Ohms lov for den komplette kæde og for sektionen af kæden: skrivning af formler, beskrivelse og forklaring
En professionel elektriker, en specialiseret elektronisk ingeniør kan ikke omgå Ohms lov i sine egne aktiviteter og løse eventuelle problemer forbundet med opsætning, indstilling, reparation af elektroniske og elektriske kredsløb.
Faktisk har alle brug for en forståelse af denne lov. Fordi alle i hverdagen har at gøre med elektricitet.
Og selvom loven fra den tyske fysiker Ohm er fastsat af et gymnasiekursus, studeres det i praksis ikke altid rettidigt. Derfor overvejer vi i vores materiale et sådant emne, der er relevant for livet, og vi vil beskæftige os med mulighederne for at skrive formlen.
Indholdet af artiklen:
Separat sektion og komplet elektrisk kredsløb
I betragtning af det elektriske kredsløb ud fra synspunktet om at anvende Ohms lov på kredsløbet skal der bemærkes to mulige beregningsmuligheder: for et enkelt afsnit og for et fuldgyldigt kredsløb.
Beregning af det aktuelle afsnit af det elektriske kredsløb
Den del af kredsløbet betragtes som regel som en del af kredsløbet, eksklusive kilden til EMF, som at have yderligere intern modstand.
Derfor ser beregningsformlen i dette tilfælde enkel ud:
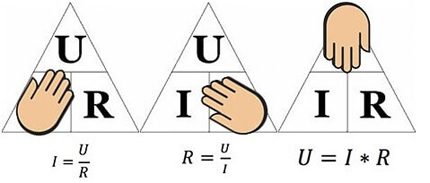
I = U / R,
Hvor:
- jeg - strømstyrke;
- U - påført spænding
- R - modstand.
Fortolkningen af formlen er enkel - strømmen, der flyder langs en bestemt del af kredsløbet, er proportional med spændingen, der påføres den, og modstanden er omvendt proportional.
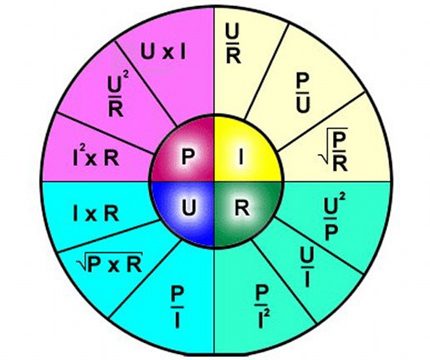
Formlen beskriver således klart afhængigheden af strømmen, der strømmer gennem et separat afsnit af det elektriske kredsløb i forhold til visse spændings- og modstandsværdier.
Det er praktisk at bruge formlen, for eksempel beregning af modstandsparametre, som skal loddes ind i kredsløbet, hvis spændingen med strøm er specificeret.
Ovenstående figur vil hjælpe med at bestemme for eksempel strømmen, der strømmer gennem en 10-ohm-modstand, hvortil en spænding på 12 volt påføres. Ved at udskifte værdierne finder vi - I = 12/10 = 1,2 ampere.
Tilsvarende løses opgaverne til at finde modstand (når strøm med spænding er kendt) eller spænding (når spænding med strøm kendes).
Det er således altid muligt at vælge den krævede driftsspænding, den krævede strømstyrke og det optimale modstandselement.
Forresten er forbindelseskablerne i ethvert kredsløb modstand. Størrelsen på den belastning, de skal bære, bestemmes af spændingen.
Følgelig, igen ved hjælp af Ohms lov, bliver det muligt nøjagtigt at vælge det nødvendige ledertværsnit, afhængigt af kernenes materiale.
Vi har detaljerede instruktioner på hjemmesiden kabeltværsnit med strøm og strøm.
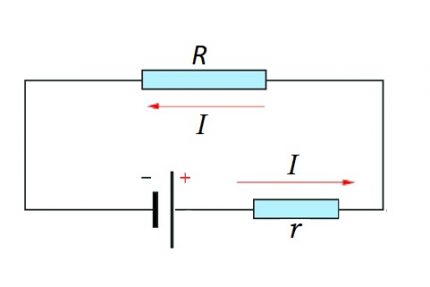
Beregningsmulighed for fuld kæde
En komplet kæde er allerede site (r) såvel som kilden til EMF. Det er faktisk, at den interne modstand fra EMF-kilden føjes til den eksisterende modstandsdygtige komponent i kredsløbsafsnittet.
Derfor er nogle ændringer til ovenstående formel logisk:
I = U / (R + r)
Værdien af EMF's interne modstand i Ohms lov for et komplet elektrisk kredsløb kan naturligvis betragtes som ubetydelig, selvom denne resistensværdi i mange henseender afhænger af strukturen af EMF-kilden.
Når man beregner komplekse elektroniske kredsløb, elektriske kredsløb med mange ledere, er tilstedeværelsen af yderligere modstand en vigtig faktor.
For både kredsløbsafsnittet og det komplette kredsløb skal der tages hensyn til det naturlige øjeblik - brugen af en konstant eller variabel strøm.
Hvis de punkter, der er nævnt ovenfor, karakteristiske for Ohms lov, blev taget i betragtning med hensyn til anvendelse af jævnstrøm, i overensstemmelse hermed med vekselstrøm ser alt lidt anderledes ud.
Overvejelse af loven til en variabel
Begrebet "modstand" mod betingelserne for vekselstrøms passage bør betragtes mere som begrebet "impedans". Dette er en kombination af den aktive resistive belastning (Ra) og belastningen dannet af den reaktive modstand (Rr).
Sådanne fænomener er forårsaget af parametre for induktive elementer og omskiftningsloverne anvendt på en variabel spændingsværdi - en sinusformet strømværdi.
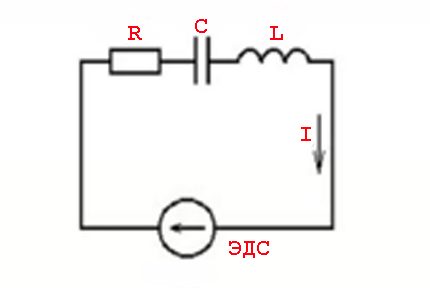
Med andre ord er der en virkning af at fremføre (hæmme) strømværdier fra spændingsværdier, som ledsages af udseendet af aktive (resistive) og reaktive (induktive eller kapacitive) kapaciteter.
Beregningen af sådanne fænomener udføres ved hjælp af formlen:
Z = U / I eller Z = R + J * (XL - XC)
hvor: Z - impedans; R - aktiv belastning; XL , XC - induktiv og kapacitiv belastning; J - koefficient.
Serier og parallel tilslutning af elementer
For elementer i et elektrisk kredsløb (kredsløbsafsnit) er et karakteristisk moment en serie eller parallel forbindelse.
Følgelig ledsages hver type forbindelse af en anden karakter af strømstrømmen og spændingsforsyningen. I denne forbindelse finder Ohms lov også anvendelse på forskellige måder, afhængigt af muligheden for at inkludere elementer.
Modstandskredsløb
I forbindelse med en seriel forbindelse (et afsnit i et kredsløb med to komponenter) anvendes følgende formel:
- I = i1 = Jeg2 ;
- U = U1 + U2 ;
- R = R1 + R2
Denne formulering viser tydeligt, at uanset antallet af resistive komponenter, der er forbundet i serie, ændrer strømmen i kredsløbet ikke.
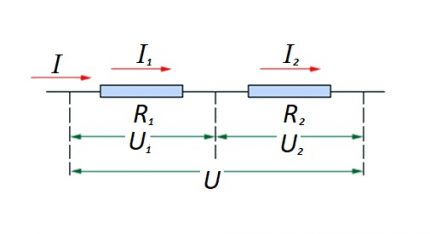
Størrelsen på spændingen, der påføres de aktive resistive komponenter i kredsløbet, er summen af den samlede værdi af emk-kilden.
Spændingen på hver enkelt komponent er lig med: Ux = I * Rx.
Den samlede modstand skal betragtes som summen af klassificeringerne for alle de resistive komponenter i kredsløbet.
Kredsløb for parallelle tilsluttede resistive elementer
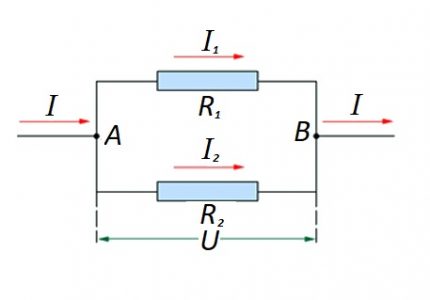
I tilfælde, hvor der er en parallel forbindelse af resistive komponenter, betragtes følgende formel som rimelig med hensyn til loven fra den tyske fysiker Ohm:
- I = i1 + Jeg2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Indstillinger til kompilering af kredsløbsafsnit af en ”blandet” type, når der bruges parallel- og seriel forbindelse, udelukkes ikke.
For sådanne indstillinger udføres beregningen normalt ved den indledende beregning af den resistive bedømmelse af den parallelle forbindelse. Derefter tilføjes værdien af den i serie forbundne modstand til resultatet.
Integrerede og differentierede retlige former
Alle ovenstående punkter med beregningerne gælder for forhold, når ledere med en "homogen" struktur anvendes i de elektriske kredsløb.
I mellemtiden må man ofte i praksis beskæftige sig med konstruktionen af et kredsløb, hvor strukturen af lederne ændrer sig i forskellige områder. F.eks. Bruges ledninger med et større tværsnit eller tværtimod mindre, fremstillet på basis af forskellige materialer.
For at redegøre for sådanne forskelle er der en variation af den såkaldte "Ohms differentielle integrale lov". For en uendelig lille leder beregnes strømtæthedsniveauet afhængigt af styrken og ledningsevnen.
Under differentieringsberegningen tages formlen: J = ό * E
Til henholdsvis integreret beregning formuleringen: I * R = φ1 - φ2 + έ
Imidlertid er disse eksempler temmelig tættere på skolen med højere matematik, og i faktisk praksis bruges faktisk ikke en simpel elektriker.
Konklusioner og nyttig video om emnet
En detaljeret analyse af Ohms lov i videoen nedenfor vil hjælpe med til endelig at konsolidere viden i denne retning.
En særegen videolektion forstærker kvalitativt den teoretiske skriftlige præsentation:
Elektrikernes arbejde eller en elektronisk ingeniørs aktivitet er uløseligt forbundet med øjeblikke, hvor du virkelig skal overholde Georg Ohms lov i handling. Dette er nogle almindelige sandheder, som enhver professionel burde kende.
Ekstensiv viden om dette spørgsmål er ikke påkrævet - det er nok at lære de tre vigtigste variationer af ordlyden for at kunne anvende i praksis.
Vil du supplere ovenstående materiale med værdifulde kommentarer eller udtrykke din mening? Skriv kommentarer i blokken under artiklen. Hvis du har spørgsmål, er du velkommen til at spørge vores eksperter.

 Sådan beregnes effekt, strøm og spænding: principper og eksempler på beregning af indenlandske forhold
Sådan beregnes effekt, strøm og spænding: principper og eksempler på beregning af indenlandske forhold  Konvertering af ampere til watt: regler og praktiske eksempler på konvertering af spænding og strømmenheder
Konvertering af ampere til watt: regler og praktiske eksempler på konvertering af spænding og strømmenheder  Sådan konverteres ampere til kilowatt: principper for oversættelse og praktiske eksempler med forklaringer
Sådan konverteres ampere til kilowatt: principper for oversættelse og praktiske eksempler med forklaringer  Uafbrudt til computeren: vurdering af den bedste UPS
Uafbrudt til computeren: vurdering af den bedste UPS  Konventioner i elektriske kredsløb: afkodning af grafik og alfanumeriske tegn
Konventioner i elektriske kredsløb: afkodning af grafik og alfanumeriske tegn  Konverter kilowatt til hestekræfter: hvor mange lægemidler i en kW + -princippet og beregningsmetoder
Konverter kilowatt til hestekræfter: hvor mange lægemidler i en kW + -princippet og beregningsmetoder  Hvor meget koster det at forbinde gas til et privat hus: prisen for at organisere gasforsyningen
Hvor meget koster det at forbinde gas til et privat hus: prisen for at organisere gasforsyningen  De bedste vaskemaskiner med tørretumbler: modelvurdering og kundetips
De bedste vaskemaskiner med tørretumbler: modelvurdering og kundetips  Hvad er lysets farvetemperatur og nuancerne ved at vælge lampernes temperatur, der passer til dine behov
Hvad er lysets farvetemperatur og nuancerne ved at vælge lampernes temperatur, der passer til dine behov  Udskiftning af en geyser i en lejlighed: papirudskiftning + grundlæggende normer og krav
Udskiftning af en geyser i en lejlighed: papirudskiftning + grundlæggende normer og krav