Ohmi törvény a teljes láncra és a lánc szakaszára: képletek írása, leírás és magyarázat

Professzionális villanyszerelő, speciális elektronikai mérnök nem tudja megkerülni az Ohm törvényét a saját tevékenységei során, megoldva az elektronikus és elektromos áramkörök felállításával, hangolásával és javításával kapcsolatos problémákat.

Valójában mindenkinek szüksége van e törvény megértésére. Mivel a mindennapi életben mindenkinek foglalkoznia kell az elektromossággal.

És bár a német fizikus Ohm törvényét középiskolai kurzus biztosítja, a gyakorlatban ezt nem mindig tanulják meg kellő időben. Ezért anyagunkban megvizsgáljuk az élet szempontjából releváns témát, és foglalkozunk a képlet megírásának lehetőségeivel.

Külön szakasz és teljes elektromos áramkör

Az elektromos áramkört az Ohmi törvénynek az áramkörre történő alkalmazásának szempontjából két lehetséges számítási lehetőséget kell megjegyezni: egy szakaszra és egy teljes értékű áramkörre.

Az elektromos áram jelenlegi szakaszának kiszámítása

Az áramkörnek azt a részét, mint szabályt, az áramkör részének tekintik, kivéve az EMF forrását, mint amelynek további belső ellenállása van.

Ezért a számítási képlet ebben az esetben egyszerűnek tűnik:

I = U / R,

Ahol:

• én - áramszilárdság;
• U - alkalmazott feszültség;
• R - ellenállás.

A képlet értelmezése egyszerű - az áramkör egy bizonyos része mentén áramló áram arányos a rá alkalmazott feszültséggel, és az ellenállás fordítottan arányos.

Az úgynevezett grafikus „százszorszép”, amelyen keresztül az Ohm törvénye alapján készítik a készítmények variációinak teljes készletét. Kényelmes eszköz a zsebtároláshoz: „P” szektor - teljesítményképletek; „U” szektor - feszültségképletek; „I” szektor - jelenlegi képletek; „R” szektor - ellenállási képletek

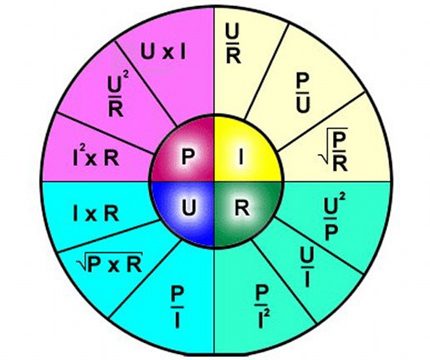
Így a képlet egyértelműen leírja az elektromos áramkör külön szakaszán átáramló áram függését a feszültség és az ellenállás bizonyos értékeihez viszonyítva.

Kényelmes a képlet segítségével kiszámítani például az ellenállási paramétereket, amelyeket be kell forrasztani az áramkörbe, ha az árammal feszültség megadva.

Ohmi törvény és két következmény, amelyek minden profi villanyszerelőnek, villamosmérnöknek, elektronikai mérnöknek és mindenkinek, akik az elektromos áramkörök munkájához kapcsolódnak, kötelezőek. Balról jobbra: 1 - áramérzékelés; 2 - az ellenállás meghatározása; 3 - feszültség meghatározás, ahol I - áramszilárdság, U - feszültség, R - ellenállás

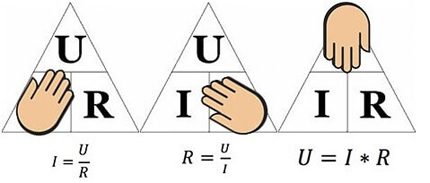
A fenti ábra segít meghatározni például egy 10 ohmos ellenálláson átáramló áramot, amelyre 12 voltos feszültséget alkalmaznak. Az értékeket helyettesítve megkapjuk - I = 12/10 = 1,2 amperes értéket.

Hasonlóképpen oldják meg az ellenállás (amikor a feszültségű áram ismert) vagy a feszültség (amikor az áram feszültsége ismert) feladatait.

Így mindig meg lehet választani a szükséges üzemi feszültséget, a szükséges áramerősséget és az optimális ellenállási elemet.

A javasolt képlet nem igényli a feszültségforrás paramétereinek figyelembevételét. Azonban egy áramkört, amely tartalmaz például egy akkumulátort, egy másik képlet alapján számítják ki. Az ábrán: A - ampermérő beépítése; V - a voltmérő beépítése.

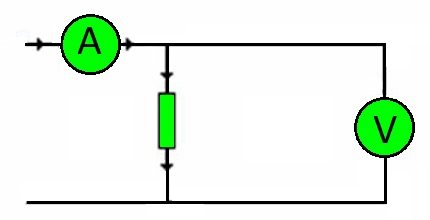
Mellesleg, az áramkör összekötő vezetékei ellenállók. A terhelés nagyságát, amelyet el kell viselniük, a feszültség határozza meg.

Ennek megfelelõen, ismét az Ohmi törvény alkalmazásával lehetõvé válik a megfelelõ vezetõ keresztmetszet pontos kiválasztása a mag anyagától függõen.

Részletes utasítások vannak a weboldalon kábel keresztmetszete áram és áram által.

Számítási lehetőség a teljes láncra

A teljes lánc már a hely (ek), valamint az EML forrása. Vagyis az EML-forrás belső ellenállása hozzáadódik az áramköri szakasz meglévő ellenálló eleméhez.

Ezért a fenti képlet néhány módosítása logikus:

I = U / (R + r)

Természetesen az EML belső ellenállásának értéke az Ohmi törvényben a teljes elektromos áramkör számára elhanyagolhatónak tekinthető, bár sok szempontból ez az ellenállás értéke az EML forrásának szerkezetétől függ.

Az összetett elektronikus áramkörök, sok vezetővel rendelkező elektromos áramkörök kiszámításakor azonban a kiegészítő ellenállás jelenléte fontos tényező.

A teljes értékű elektromos áramkörben végzett számításoknál az EML-forrás ellenállási értékét mindig figyelembe kell venni. Ezt az értéket hozzáadja maga az elektromos áramkör ellenállása. Az ábrán: I - áramáram; R a külső ellenállás elem; r az EMF (energiaforrás) ellenállási tényezője

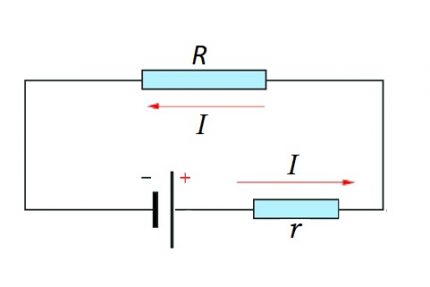
Mind az áramköri szakasz, mind a teljes áramkör esetében figyelembe kell venni a természetes nyomatékot - állandó vagy változó áram használata.

Ha az Ohm törvényére jellemző fent említett pontokat egyenáram felhasználásának szempontjából vettük figyelembe, akkor a váltakozó árammal minden kicsit másképp néz ki.

A törvény figyelembevétele változóra

A váltakozó áram áthaladásának feltételeivel szembeni ellenállás fogalmát inkább az "impedancia" fogalmának kell tekinteni. Ez az aktív ellenállási terhelés (Ra) és a reaktív ellenállás (Rr) által létrehozott terhelés kombinációja.

Az ilyen jelenségeket az induktív elemek paraméterei és a változó feszültségértékre - szinuszos áramértékre - történő kapcsolás törvényei okozzák.

Úgy tűnik, hogy ez egy váltakozó áramú elektromos áramkör ekvivalens áramköre az Ohmi törvény alapelvein alapuló formulációk felhasználásával történő számításhoz: R - ellenállású komponens; C a kapacitív komponens; L az induktív komponens; Az EML energiaforrás; I-áram áramlás

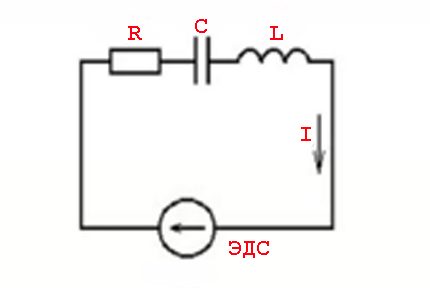
Más szavakkal, az áramértékek előrelépése (lemaradása) a feszültségértékektől függ, amelyet az aktív (ellenállás) és a reaktív (induktív vagy kapacitív) kapacitások megjelenése kísér.

Az ilyen jelenségek kiszámítása a következő képlet alapján történik:

Z = U / I vagy Z = R + J * (X_L - X_C)

ahol: Z - impedancia; R - aktív terhelés; X_L , X_C - induktív és kapacitív terhelés; J - együttható.

Az elemek soros és párhuzamos csatlakoztatása

Az elektromos áramkör (áramköri szakasz) elemeinek jellemzõ nyomatéka soros vagy párhuzamos csatlakozás.

Ennek megfelelően az egyes csatlakozástípusokhoz az áramáram és a feszültség eltérő jellege társul. E tekintetben az Ohmi törvény különböző módon is alkalmazandó, az elemek beillesztésének lehetőségétől függően.

Ellenállás áramköre

A soros csatlakozáshoz (egy áramkörnek egy két részből álló része) a következő képletet kell használni:

• I = i₁ = Én₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Ez a megfogalmazás egyértelműen igazolja, hogy függetlenül a sorosan csatlakoztatott ellenálló elemek számától, az áramkörben áramló áram nem változik.

Az ellenállás elemek egymás után sorba kapcsolása az áramköri szakaszban. Erre a lehetőségre a saját számítási törvénye vonatkozik. Az ábrán: I, I1, I2 - áramáram; R1, R2 - ellenálló elemek; U, U1, U2 - alkalmazott feszültség

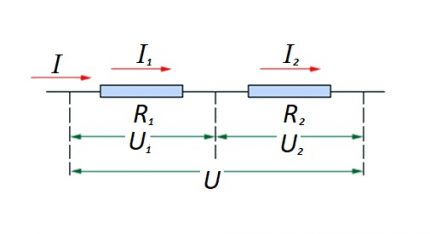
Az áramkör aktív ellenálló elemeire alkalmazott feszültség nagysága az EMF forrás teljes értékének összege.

Az egyes komponensek feszültsége egyenlő: Ux = I * Rx.

A teljes ellenállást az áramkör minden ellenálló elemének névleges összegeként kell figyelembe venni.

Párhuzamosan kapcsolt ellenállás elemek áramköre

Abban az esetben, ha az ellenálló elemek összekapcsolódnak, az alábbi képlet méltányossá válik a német fizikus Ohm törvénye szempontjából:

• I = i₁ + Én₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

A „vegyes” áramköri szakaszok összeállításának lehetőségei párhuzamos és soros csatlakozás esetén nem zárhatók ki.

Az ellenállás elemek összekapcsolása az áramkörben egymással párhuzamosan. Erre a lehetőségre a saját számítási törvényét kell alkalmazni. Az ábrán: I, I1, I2 - áramáram; R1, R2 - ellenálló elemek; U az összesített feszültség; A, B - belépési / kilépési pontok

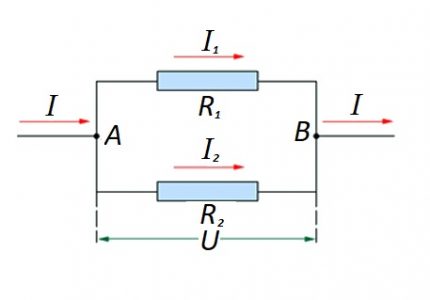
Ilyen opciók esetén a számítást általában a párhuzamos csatlakozás ellenállásának kezdeti számításával végzik el. Ezután a sorba kapcsolt ellenállás értékét hozzáadjuk az eredményhez.

Integrált és differenciált jogi formák

A számítások fenti pontjai vonatkoznak olyan körülményekre, amikor „homogén” szerkezetű vezetőket használnak az elektromos áramkörökben.

Eközben a gyakorlatban gyakran kell egy olyan áramkör felépítésével foglalkozni, ahol a vezetők szerkezete különböző területeken változik. Például nagyobb keresztmetszetű huzalokat, vagy éppen ellenkezőleg, kisebb anyagokat használnak, amelyek különböző anyagokból készültek.

Az ilyen különbségek figyelembevétele érdekében megváltoztatható az úgynevezett "Ohmi differenciális integrál törvény". Végtelen kis vezető esetén az áram sűrűségét az erősségtől és a vezetőképességtől függően kell kiszámítani.

A differenciális számítás során a következő képletet veszik figyelembe: J = ό * E

Az integrált számításhoz a következő megfogalmazást: I * R = φ1 - φ2 + έ

Ezek a példák azonban inkább közelebb állnak a felső matematika iskolájához, és a gyakorlatban nem használnak egyszerű villanyszerelőt.

Következtetések és hasznos videó a témáról

Az alábbi videóban szereplő Ohm-törvény részletes elemzése segít véglegesen megszilárdítani az ismereteket ebben az irányban.

Egy sajátos videotéma minőségileg megerősíti az elméleti írásbeli prezentációt:

Villanyszerelő munkája vagy elektronikus mérnök tevékenysége elválaszthatatlanul összekapcsolódik azokkal a pillanatokkal, amikor ténylegesen be kell tartania a Georg Ohm törvényét. Ez néhány általános igazság, amelyet minden szakembernek tudnia kell.

Ebben a kérdésben nem szükséges széles körű ismerete - elegendő megtanulni a megfogalmazás három fő változatát, hogy sikeresen alkalmazható legyen a gyakorlatban.

Kiegészíteni szeretné a fenti anyagot értékes megjegyzésekkel, vagy kifejezni véleményét? Kérjük, írjon megjegyzéseket a cikk alatt található blokkba. Ha bármilyen kérdése van, kérjük, bátran forduljon szakértőinkhez.