Beregning av kabeltverrsnitt etter strøm og strøm: hvordan beregne ledninger riktig
Planlegger du å gjøre det modernisering av strømnettet eller i tillegg til å utvide kraftledningen til kjøkkenet for å koble til en ny elektrisk komfyr? Her er minimal kunnskap om lederens tverrsnitt og effekten av denne parameteren på effekt og strømstyrke.
Enig i at feil beregning av kabeltverrsnittet fører til overoppheting og kortslutning eller til uberettigede kostnader.
Det er veldig viktig å utføre beregninger på prosjekteringsstadiet, siden feilen i skjult ledningsnett og etterfølgende utskifting er full av betydelige kostnader. Vi hjelper deg med å håndtere forviklingene i beregningene for å unngå problemer under videre drift av strømnettet.
For ikke å belaste deg med komplekse beregninger, valgte vi forståelige formler og beregningsalternativer, ga informasjon i en tilgjengelig form, og ga formlene forklaringer. Tematiske bilder og videomateriell ble også lagt til artikkelen, som gjør det mulig å forstå essensen av saken som er under behandling.
Innholdet i artikkelen:
Beregning av tverrsnittet etter forbrukernes kraft
Hovedformålet med lederne er levering av elektrisk energi til forbrukerne i ønsket mengde. Siden superledere ikke er tilgjengelige under normale driftsforhold, må motstanden til ledermaterialet tas i betraktning.
Beregning av den nødvendige delen ledere og kabler avhengig av forbrukernes totale kapasitet basert på langvarig driftserfaring.
Vi begynner den generelle beregningsprosessen ved først å utføre beregningene ved å bruke formelen:
P = (P1 + P2 + .. PN) * K * J,
der:
- P - kraften til alle forbrukere koblet til den beregnede filialen i Watts.
- P1, P2, PN - kraften til den første forbrukeren, henholdsvis den andre, n-th, i Watts.
Etter å ha mottatt resultatet på slutten av beregningene i henhold til formelen ovenfor, var det på tide å vende seg til tabelldataene.
Nå må du velge den nødvendige delen i henhold til tabell 1.
Fase 1 - beregning av reaktiv og aktiv kraft
Forbrukernes kapasitet er angitt i dokumentene for utstyret. Vanligvis indikerer utstyrsnivået aktiv effekt sammen med reaktiv kraft.
Enheter med en aktiv type belastning forvandler all mottatt elektrisk energi, tatt i betraktning effektiviteten, til nyttig arbeid: mekanisk, termisk eller dens andre form.
Enheter med aktiv belastning inkluderer glødelamper, varmeovner og elektriske ovner.
For slike enheter har beregningen av strøm for strøm og spenning formen:
P = U * I,
der:
- P - kraft i watt;
- U - spenning i V;
- jeg - strømstyrke i A.
Enheter med en reaktiv type belastning kan akkumulere energi fra kilden og deretter returnere den. En slik utveksling skjer på grunn av forskyvningen av sinusformet strøm og sinusformet spenning.
Reaktive kraftapparater inkluderer elektriske motorer, elektroniske enheter i alle størrelser og formål og transformatorer.
Elektriske nettverk er bygget på en slik måte at de kan overføre elektrisk energi i en retning fra kilden til lasten.
Derfor er den returnerte energien til forbrukeren med en reaktiv belastning parasittisk og brukes på varmeledere og andre komponenter.
Reaktiv effekt er avhengig av fasevinkelen mellom spenningen og sinusoidene. Fasevinkelen er uttrykt i form av cosφ.
For å finne full effekt, bruk formelen:
P = Q / cosφ,
hvor Q - reaktiv kraft i VA.
Vanligvis indikerer passdataene på enheten reaktiv kraft og cosφ.
eksempel: i passet viser perforatoren en reaktiv effekt på 1200 VAR og cosφ = 0,7. Derfor vil det totale strømforbruket være lik:
P = 1200 / 0,7 = 1714 W
Hvis ikke cos not kunne bli funnet, for det store flertallet av elektriske husholdningsapparater, kan cosφ tas lik 0,7.
Fase 2 - søk etter forhold og marginalforhold
K - dimensjonsløs samtidighetskoeffisient, viser hvor mange forbrukere som samtidig kan inkluderes i nettverket. Det hender sjelden at alle enheter samtidig bruker strøm.
Samtidig drift av TV- og musikksenteret er usannsynlig. Fra etablert praksis kan K tas lik 0,8. Hvis du planlegger å bruke alle forbrukere samtidig, bør K tas lik 1.
J - dimensjonsløs sikkerhetsfaktor. Det kjennetegner etableringen av en maktreserve for fremtidige forbrukere.
Fremdriften står ikke stille, hvert år blir det oppfunnet nye og overraskende nye og nyttige elektriske apparater. Innen 2050 forventes strømforbruket å nå 84%. Typisk antas J å være fra 1,5 til 2,0.
Fase 3 - utføre en geometrisk beregning
I alle elektriske beregninger tas lederens tverrsnittsareal - kjernesnittet. Målt i mm2.
Det er ofte nødvendig å lære å beregne riktig ledningsdiameter ledningsleder.
I dette tilfellet er det en enkel geometrisk formel for en monolitisk rund ledning:
S = π * R2 = π * D2/4eller omvendt
D = √ (4 * S / π)
For ledere med rektangulært tverrsnitt:
S = h * m,
der:
- S - kjerneområde i mm2;
- R - kjernens radius i mm;
- D - kjernediameter i mm;
- h, m - henholdsvis bredde og høyde i mm;
- π Er tallet pi lik 3,14.
Hvis du kjøper en strandet ledning, der en leder består av mange vridde ledninger med sirkulært tverrsnitt, utføres beregningen i henhold til formelen:
S = N * D2/1,27,
hvor N - antall ledninger i venen.
Ledninger som har vridde kjerner på flere ledninger har generelt bedre ledningsevne enn monolitiske ledninger. Dette skyldes særegenhetene til strømmen som strømmer gjennom en sirkulær leder.
Elektrisk strøm er bevegelsen av de samme ladningene langs lederen. Ladningene med samme navn frastøter, derfor blir ladefordelingsdensiteten forskjøvet til overflaten av lederen.
En annen fordel med strandede ledninger er deres fleksibilitet og mekaniske motstand. Monolitiske ledninger er billigere og brukes hovedsakelig til fast installasjon.
Fase 4 - beregne kraftseksjonen i praksis
oppgave: den totale kraften til forbrukere på kjøkkenet er 5000 watt (noe som betyr at kraften til alle reaktive forbrukere blir fortalt). Alle forbrukere er koblet til et enfase 220 V-nettverk og har strøm fra en gren.
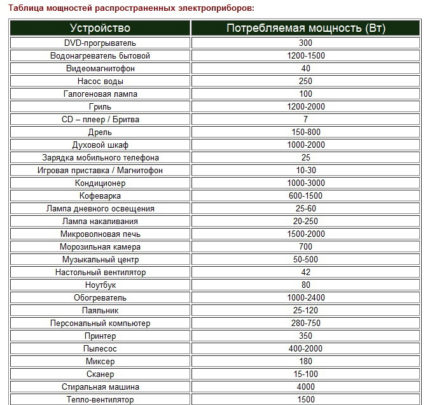
beslutning:
Samtidighetskoeffisienten K antas å være lik 0,8. Kjøkkenet er et sted for konstant innovasjon, det er ikke noe for deg, en sikkerhetsfaktor på J = 2,0. Total estimert kapasitet vil være:
P = 5000 * 0,8 * 2 = 8000 W = 8 kW
Ved å bruke verdien på designkraften ser vi etter den nærmeste verdien i tabell 1.
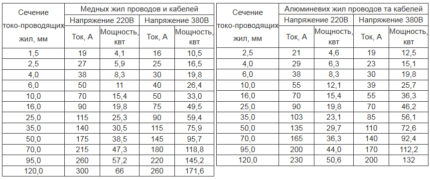
Det nærmeste egnede ledertverrsnitt for et enfase-nettverk er en kobberleder med et tverrsnitt på 4 mm2. Lignende trådstørrelse med aluminiumskjerne 6 mm2.
For ledninger med enkelkjernen vil minimum diameteren være henholdsvis 2,3 mm og 2,8 mm. Når det gjelder et flerkjernes alternativ, legges tverrsnittet av individuelle kjerner opp.
Beregning av gjeldende tverrsnitt
Beregninger av nødvendig tverrsnitt for strøm og strøm av kabler og ledninger vil gi mer nøyaktige resultater. Slike beregninger gjør det mulig å evaluere den generelle effekten av forskjellige faktorer på ledere, inkludert termisk belastning, trådkvalitet, type pakning, driftsforhold, etc.
Hele beregningen blir utført under følgende trinn:
- maktvalg av alle forbrukere;
- beregning av strømmer som går gjennom lederen;
- valg av passende tverrsnitt i henhold til tabellene.
For denne versjonen av beregningen tas strømmen til forbrukere med spenning uten å ta hensyn til korreksjonsfaktorer. De vil bli tatt hensyn til når du summerer dagens styrke.
Trinn 1 - beregning av gjeldende styrke med formlene
For de som har glemt skolefysikkurs, tilbyr vi de grunnleggende formlene i form av et grafisk diagram som et visuelt jukseark:
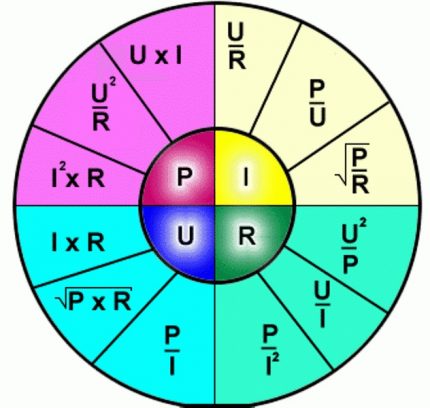
La oss skrive avhengigheten av strømstyrken I av kraften P og linjespenningen U:
I = P / Ul,
der:
- jeg - strømstyrke, tatt i ampere;
- P - kraft i watt;
- Ul - ledningsspenning i volt.
Lineær spenning avhenger generelt av strømforsyningskilden, den er en- og trefaset.
Forholdet mellom den lineære og fasespenningen:
- Ul = U * cosφ i tilfelle enfasespenning.
- Ul = U * √3 * cosφ i tilfelle trefasespenning.
For elektriske husholdningsforbrukere, ta cosφ = 1, slik at den lineære spenningen kan skrives om:
- Ul = 220 V for enfasespenning.
- Ul = 380 V for trefasespenning.
Deretter oppsummerer vi alle strømningene som forbrukes av formelen:
I = (I1 + I2 + ... IN) * K * J,
der:
- jeg - total strøm i ampere;
- I1..IN - gjeldende styrke for hver forbruker i ampere;
- K - samtidighetskoeffisient;
- J - sikkerhetsfaktor.
Koeffisientene K og J har de samme verdiene som ble brukt for å beregne den totale effekten.
Det kan være tilfelle når det strømmer seg i ulik styrke i et trefaset nettverk gjennom forskjellige faseledere.
Dette skjer når enfasekonsumenter og trefasekonsumenter kobles til en trefasekabel samtidig. For eksempel drives en trefaset maskin og enfasebelysning.
Et naturlig spørsmål oppstår: hvordan beregnes tverrsnittet av en strandet ledning i slike tilfeller? Svaret er enkelt - beregningene er gjort for den mest lastede lederen.
Trinn 2 - velg et passende avsnitt i henhold til tabellene
I reglene for drift av elektriske installasjoner (PES) er det gitt et antall tabeller for valg av ønsket kabelkjernedel.
Ledningsevne er temperaturavhengig. For metallledere øker motstanden med økende temperatur.
Når en viss terskel overskrides, blir prosessen selvopprettholdt: jo høyere motstand, jo høyere temperatur, desto høyere er motstand osv. til lederen brenner ut eller forårsaker kortslutning.
Følgende to tabeller (3 og 4) viser tverrsnittet av lederne avhengig av strømmer og installasjonsmåte.
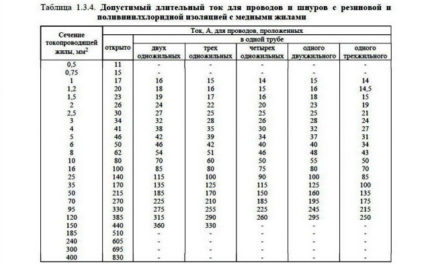
Kabelen skiller seg fra ledningen ved at alle ledningene med egen isolasjon på kabelen er vridd inn i en bunt og lukket i et felles isolasjonsmantel. Flere detaljer om forskjeller og typer kabelprodukter er skrevet i dette artikkel.
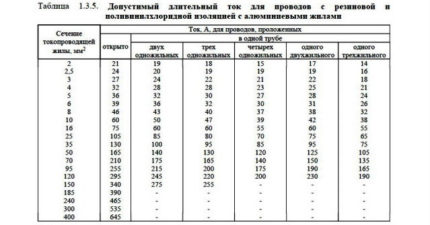
Ved bruk av tabeller brukes følgende faktorer på den tillatte kontinuerlige strømmen:
- 0,68 hvis 5-6 levde;
- 0,63 hvis 7-9 levde;
- 0,6 hvis 10-12 levde.
Synkende koeffisienter brukes til gjeldende verdier fra den "åpne" kolonnen.
Null- og jordingsledere er ikke inkludert i antall ledere.
I henhold til PES-standarder gjøres valget av tverrsnittet av nullkjernen i henhold til den tillatte kontinuerlige strømmen som minst 50% av fasekjernen.
Følgende to tabeller (5 og 6) viser avhengigheten av den tillatte kontinuerlige strømmen når du legger den i bakken.
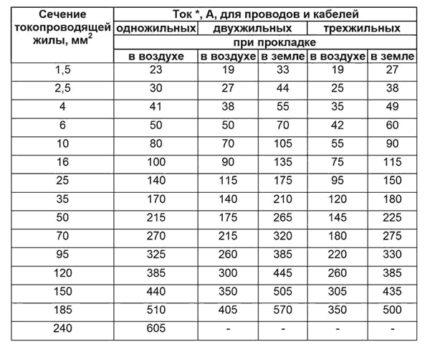
Strømbelastningen når den legges åpen og når den dypes ned i bakken er forskjellig. De blir likestilt hvis legging i bakken utføres ved hjelp av brett.
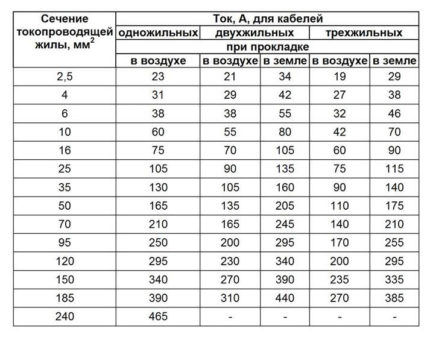
Følgende tabell (7) gjelder ordningen av midlertidige kraftforsyningsledninger (frakt, hvis for privat bruk).
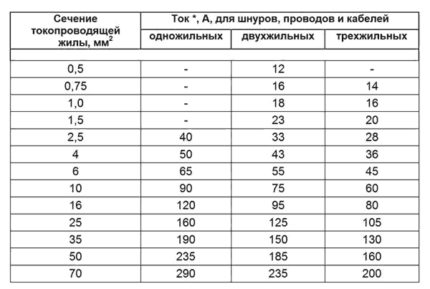
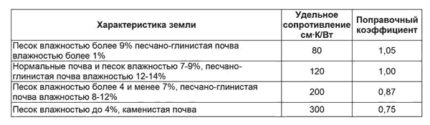
Når du legger kabler i bakken, i tillegg til varmefjerningsegenskaper, er det nødvendig å ta hensyn til resistiviteten, noe som gjenspeiles i følgende tabell (8):
Beregning og valg av kobberledere opp til 6 mm2 eller aluminium opp til 10 mm2 ledet som for kontinuerlig strøm.
Ved store tverrsnitt er det mulig å bruke en reduksjonsfaktor:
0,875 * √Tns
hvor Tns - forholdet mellom varigheten av inkluderingen og syklusens varighet.
Varigheten av inkludering er hentet fra beregningen på ikke mer enn 4 minutter. I dette tilfellet bør syklusen ikke overstige 10 minutter.
Når du velger en kabel for kabling til strøm trehus spesiell oppmerksomhet rettes mot dens brannmotstand.
Trinn 3 - beregning av tverrsnittet til strømlederen ved hjelp av et eksempel
oppgave: beregne det nødvendige tverrsnittet kobberkabel for å koble til:
- 4000 W tre-fase trebearbeidingsmaskin;
- 6000 W trefaset sveisemaskin;
- husholdningsapparater i huset med en total kapasitet på 25.000 watt;
Tilkoblingen vil skje med en femkjernekabel (trefase ledere, en nøytral og en jord) som er lagt i bakken.

Beslutning.
Trinn 1. Vi beregner den lineære spenningen til en trefasetilkobling:
Ul = 220 * √3 = 380 V
Trinn 2. Husholdningsapparater, maskinverktøy og sveisemaskiner har reaktiv kraft, så kraften til maskiner og utstyr vil være:
Pav de = 25000 / 0,7 = 35700 W
PEqui = 10000 / 0,7 = 14300 W
Trinn 3. Gjeldende strøm for å koble til husholdningsapparater:
jegav de = 35700/220 = 162 A
Trinn 4. Gjeldende strøm for å koble til utstyr:
jegEqui = 14300/380 = 38 A
Trinn 5. Den nødvendige strømmen for tilkobling av husholdningsapparater beregnes ut fra beregningen av en fase. Avhengig av problemets tilstand er det tre faser. Følgelig kan strømmen fordeles i faser. For enkelhets skyld antar vi en enhetlig fordeling:
jegav de = 162/3 = 54 A
Trinn 6. Nåværende per fase:
jegf = 38 + 54 = 92 A
Trinn 7 Utstyr og husholdningsapparater vil ikke fungere på samme tid, bortsett fra for dette vil vi legge en margin lik 1,5. Etter anvendelse av korreksjonsfaktorer:
jegf = 92 * 1,5 * 0,8 = 110 A
Trinn 8. Selv om kabelen inneholder 5 kjerner, er det bare tatt hensyn til trefasekjerner. I følge tabell 8, i en søyle av en tre-kjernekabel i bakken, finner vi at en strøm på 115 A tilsvarer et tverrsnitt av en kjerne på 16 mm2.
Trinn 9. I følge tabell 8 bruker vi korreksjonsfaktoren avhengig av jordens egenskaper. For en vanlig landtype er koeffisienten 1.
Trinn 10. Valgfritt, beregne kjernediameteren:
D = √ (4 * 16 / 3,14) = 4,5 mm
Hvis beregningen bare ble gjort med kraft, uten å ta hensyn til kabelfunksjonene, vil tverrsnittet av kjernen være 25 mm2. Beregning av strømstyrken er mer komplisert, men noen ganger sparer det betydelige penger, spesielt når det gjelder multikjernekabler.
Du kan lese mer om forholdet mellom spenning og strøm her.
Beregning av spenningsfall
Enhver leder, unntatt superledere, har motstand. Derfor, med tilstrekkelig lengde på kabelen eller ledningen, oppstår et spenningsfall.
PES-standarder krever at tverrsnittet av kabelkjernen er slik at spenningsfallet ikke er mer enn 5%.
Dette gjelder primært lavspentkabler med lite tverrsnitt.
Beregningen av spenningsfallet er som følger:
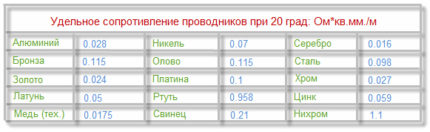
R = 2 * (ρ * L) / S,
Upad = I * R,
U% = (Upad / Uling) * 100,
der:
- 2 - koeffisient på grunn av at strømmen nødvendigvis flyter i to kjerner;
- R - ledermotstand, Ohm;
- ρ - spesifikk motstand fra lederen, Ohm * mm2/ m;
- S - ledertverrsnitt, mm2;
- Upad - spenningsfall, V;
- U% - spenningsfall med hensyn til Uling,%.
Ved å bruke formler kan du uavhengig utføre nødvendige beregninger.
Eksempel på beregning
oppgave: beregne spenningsfallet for en kobbertråd med et tverrsnitt av en kjerne på 1,5 mm2. En ledning er nødvendig for å koble til en enfaset elektrisk sveisemaskin med en total effekt på 7 kW. Ledningslengde 20 moh.
løsning:
Trinn 1. Vi beregner motstanden til kobbertråden ved å bruke tabell 9:
R = 2 * (0,0175 * 20) / 1,5 = 0,47 Ohm
Trinn 2. Strømmen som strømmer langs lederen:
I = 7000/220 = 31,8 A
Trinn 3. Spenningsfall på ledningen:
Upad = 31,8 * 0,47 = 14,95 V
Trinn 4. Vi beregner prosentandelen av spenningsfall:
U% = (14,95 / 220) * 100 = 6,8%
Konklusjon: for å koble sammen sveisemaskinen, er det nødvendig med en leder med stort tverrsnitt.
Konklusjoner og nyttig video om emnet
Beregningen av lederens tverrsnitt med formlene:
Anbefalinger fra spesialister om valg av kabel- og ledningsprodukter:
Ovennevnte beregninger gjelder for kobber- og aluminiumledere til industriell bruk. For andre typer ledere er den totale varmeoverføringen forhåndsberegnet.
Basert på disse dataene beregnes den maksimale strømmen som kan strømme gjennom lederen uten å forårsake overdreven oppvarming.
Hvis du har spørsmål om metodikken for beregning av kabeltverrsnittet eller hvis du vil dele personlig erfaring, vennligst legg igjen kommentarer til denne artikkelen. Tilbakemeldingsboksen ligger nedenfor.

 Ledningstverrsnitt for ledningsnett: hvordan du beregner riktig
Ledningstverrsnitt for ledningsnett: hvordan du beregner riktig  Hvordan lede ledninger i leiligheten med egne hender fra skjoldet: grunnleggende ordninger og regler + installasjonstrinn
Hvordan lede ledninger i leiligheten med egne hender fra skjoldet: grunnleggende ordninger og regler + installasjonstrinn  Hvordan og med hva du skal vegge veggene for kabling: orientering om byggearbeidet
Hvordan og med hva du skal vegge veggene for kabling: orientering om byggearbeidet  Korrugering for elektriske ledninger: hvordan velge og installere en korrugerte hylse for kabel
Korrugering for elektriske ledninger: hvordan velge og installere en korrugerte hylse for kabel  Stripper for stripping ledninger: regler for valg av et verktøy for stripping kabel og ledninger
Stripper for stripping ledninger: regler for valg av et verktøy for stripping kabel og ledninger  Hvilken ledning som skal brukes til kabling i huset: anbefalinger for valg
Hvilken ledning som skal brukes til kabling i huset: anbefalinger for valg  Hvor mye koster det å koble gass til et privat hus: prisen for å organisere gasstilførsel
Hvor mye koster det å koble gass til et privat hus: prisen for å organisere gasstilførsel  De beste vaskemaskinene med tørketrommel: modellvurdering og kundetips
De beste vaskemaskinene med tørketrommel: modellvurdering og kundetips  Hva er lysets fargetemperatur og nyansene ved å velge temperaturen på lampene som passer dine behov
Hva er lysets fargetemperatur og nyansene ved å velge temperaturen på lampene som passer dine behov  Utskifting av en geyser i en leilighet: utskiftende papirer + grunnleggende normer og krav
Utskifting av en geyser i en leilighet: utskiftende papirer + grunnleggende normer og krav
Ærlig talt forsto jeg ikke for hvem denne artikkelen er ment ... så mange teoretiske materialer. I hverdagen, når du velger et tverrsnitt av ledninger til en person, er en omtrentlig lastekraft av interesse, det vil si at du trenger å vite strømstyrken og hvilken del av en ledning eller kabel du må ta basert på forventet belastning. Én tabell med tverrsnitt og strømbelastning ville være nok. Råd om hvordan du korrekt bestemmer tverrsnittet av ledningen, ville ikke skade.
Likevel forsto jeg ikke hvordan jeg skulle finne den tillatte trådlengden og beregne motstanden til den samme ledningen.
Et utmerket innlegg og når jeg beregnet tverrsnittet av kabelen, første gang jeg møtte denne - bokmerke jeg den. (Teorien om hva og hvor, må du vite.) Men etter min mening er det for vanskelig for en nybegynnet elektriker og en uavhengig eier av huset.For praktiske beregninger bruker jeg ganske gode programmer, etter min mening: det er veldig enkle alternativer for grove beregninger og mer kompliserte med et økt antall angitte parametere. Og dette er som regel ganske nok.
For de som har passende utdanning, er artikkelen god, så å si, "på lappen." Men for folk som bare vil velge ledningsstørrelse for ledningsnett, er det for mye informasjon. Det viktigste er å følge de grunnleggende reglene når du beregner - ta alltid med en margin. Og slik at maskinen som den valgte ledningen går til tilsvarer den tillatte strømmen. Og det skjer, ledningen smelter allerede, og maskinen tenkte ikke engang å kutte den av.
Artikkelen, utformet som en guide til masteren for beregning av elektriske hjemmenettverk, inneholder en stor mengde referansedata, vil jeg si, til og med en veldig stor. Hvorfor overbelaste menneskets hjerne med unødvendig informasjon? For hvert elektrisk apparat som brukes i hverdagen, er klassifiseringseffekten indikert (i instruksjonene eller på bakveggen). Og i leilighetene våre et vanlig, nesten standard sett: kjøleskap (to), elektrisk komfyr, TV (tre-fire), datamaskin (bærbar PC), og så videre. Det vil si at vi har alle dataene for beregning av nettverket. 50% satt for fremtidige anskaffelser. Det er alt! Den tillatte strømbelastningen tas lik 10A, og ikke 20, ledningene vil ikke varme opp.
Nå er det viktigste! Forfatteren blandet sammen aktiv og reaktiv kraft !!! Aktiv strøm forbrukes av: ledninger, varmeovner, moderne TV-er, datamaskiner, energisparende og LED-pærer og sveisemaskiner (Sic!). Og reaktiv kraft er skjebnen til kondensatorer og induktorer, som i moderne hjem nesten er borte, så den kan ignoreres. For informasjon, strømmålere fører oversikt over AKTIV KRAFT. Den mytiske kos f for huset er nesten lik en (0,7 ville blitt så tumlet ned tidligere). Det siste jeg ønsket å si, prøv å bruke ledninger og kabler av kobber, forbindelsen deres i terminalblokkene svekkes ikke med tiden, noe som ikke kan sies for flerkjernede. Jeg håper noen forenklet oppgaven.