Gassforbruk for oppvarming av et hus 200 m²: bestemmelse av kostnader ved bruk av hoved- og flaskeolje

Eiere av mellomstore og store hytter må planlegge kostnadene for å opprettholde boliger. Derfor oppstår oppgaven ofte med å beregne gassforbruket for oppvarming av et hus 200 m² eller større område. Den originale arkitekturen lar deg vanligvis ikke bruke metodene til analogier og finne ferdige beregninger.

Det er imidlertid ikke nødvendig å betale penger for å løse dette problemet. Alle beregninger kan gjøres uavhengig av hverandre. Dette vil kreve kunnskap om visse forskrifter, samt forståelse av fysikk og geometri på skolenivå.

Vi hjelper deg med å finne ut av denne viktige saken for en hjemmeøkonom. Vi viser deg med hvilke formler beregningene er gjort, hvilke egenskaper du trenger å vite for å få resultatet. Artikkelen vi har presentert gir eksempler på bakgrunn av hvilke det vil være lettere å gjøre din egen beregning.

Finne verdien av energitap

For å bestemme mengden energi som et hus mister, er det nødvendig å kjenne til de klimatiske egenskapene til området, den termiske ledningsevnen til materialer og ventilasjonshastigheten. Og for å beregne det nødvendige volumet av gass, er det nok å vite dens brennverdi. Det viktigste i dette arbeidet er oppmerksomhet på detaljer.

Å varme opp en bygning skal kompensere for varmetap som oppstår av to hovedgrunner: varmelekkasje rundt omkretsen av huset og tilstrømningen av kald luft gjennom ventilasjonssystemet. Begge disse prosessene er beskrevet av matematiske formler, i henhold til hvilke du uavhengig kan utføre beregninger.

Varmeledningsevne og termisk motstand for materialet

Ethvert materiale kan lede varme. Intensiteten av transmisjonen uttrykkes gjennom koeffisienten for varmeledningsevne λ (W / (m × ° C)). Jo lavere den er, jo bedre er strukturen beskyttet mot frysing om vinteren.

Oppvarmingskostnadene avhenger av den termiske ledningsevnen til materialet huset skal bygges fra. Dette er spesielt viktig for de "kalde" områdene i landet.

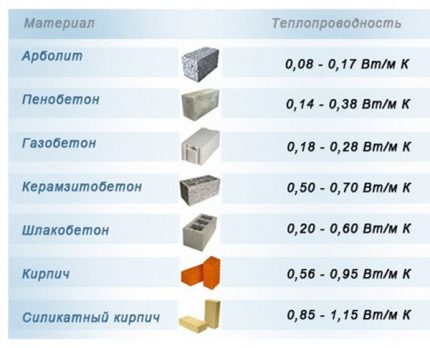
Imidlertid kan bygninger brettes eller isoleres med materialer i forskjellige tykkelser. Derfor, i praktiske beregninger, brukes varmeoverføringsmotstandskoeffisienten:

R (m² × ° C / W)

Det er assosiert med varmeledningsevne ved følgende formel:

R = h / λ,

hvor h - materialtykkelse (m).

Et eksempel. Vi bestemmer koeffisienten for motstand mot varmeoverføring av luftede betongblokker av forskjellig bredde av merket D700 kl λ = 0.16:

• bredde 300 mm: R = 0.3 / 0.16 = 1.88;
• bredde 400 mm: R = 0.4 / 0.16 = 2.50.

for isolasjonsmaterialer og vindusblokker kan gis både koeffisienten for varmeledningsevne og koeffisienten for motstand mot varmeoverføring.

Hvis den omsluttende strukturen består av flere materialer, blir koeffisientene til de enkelte lag oppsummert når du bestemmer resistensskoeffisienten mot varmeoverføring av hele "kaken".

Et eksempel. Veggen er bygget av luftede betongblokker (λ_b = 0,16), 300 mm tykk. Utenfor er det isolert ekstrudert polystyrenskum (λ_p = 0,03) 50 mm tykt og foret med fôr fra innsiden (λ_v = 0,18), 20 mm tykk.

Det er tabeller for forskjellige regioner der minimumsverdiene for den totale varmeoverføringskoeffisienten for husets omkrets er foreskrevet. De er rådgivende i sin natur.

Nå kan du beregne den totale motstandskoeffisienten mot varmeoverføring:

R = 0.3 / 0.16 + 0.05 / 0.03 + 0.02 / 0.18 = 1.88 + 1.66 + 0.11 = 3.65.

Bidraget fra lag som er ubetydelige i parameteren "varmebesparende" kan overses.

Beregning av varmetap gjennom byggekonvolutter

Varmetap Q (W) gjennom en homogen overflate kan beregnes som følger:

Q = S × dT / R,

der:

• S - areal av den betraktede overflaten (m²);
• dT - temperaturforskjell mellom luften i og utenfor rommet (° C);
• R - overflatevarmeoverføringskoeffisient (m² * ° C / W).

For å bestemme den totale indikatoren for alle varmetap, utfør følgende handlinger:

1. tildele områder som er enhetlige i motstandskoeffisienten mot varmeoverføring;
2. beregne arealet;
3. bestemme indikatorene for termisk motstand;
4. beregne varmetap for hvert av nettstedene;
5. oppsummer de oppnådde verdiene.

Et eksempel. Hjørnerom 3 × 4 meter i toppetasjen med kaldt loft. Den endelige takhøyden er 2,7 meter. Det er 2 vinduer som måler 1 × 1,5 m.

Vi finner varmetapet gjennom omkretsen ved en lufttemperatur inne i “+25 ° С”, og utenfor “–15 ° С”:

1. La oss skille ut seksjoner som er ensartet i motstandskoeffisient: tak, vegg, vinduer.
2. Takareal S_n = 3 × 4 = 12 moh². Vindusområdet S_omtrent = 2 × (1 × 1,5) = 3 moh². Veggområdet S_med = (3 + 4) × 2.7 – S_omtrent = 29,4 moh².
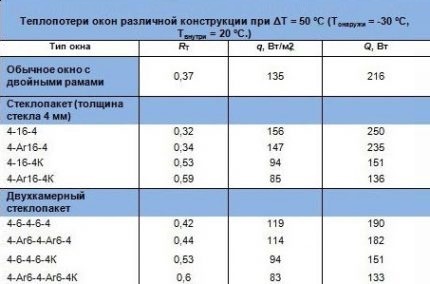
3. Koeffisienten for termisk motstand i taket er sammensatt av overlappingsindeksen (bordtykkelse 0,025 m), isolasjon (mineralullsplater 0,10 m tykk) og tregulvet på loftet (tre og kryssfiner med en total tykkelse på 0,05 m): R_n = 0,025 / 0,18 + 0,1 / 0,037 + 0,05 / 0,18 = 3,12. For vinduer tas verdien fra passet til et dobbeltvindus med to kammer: R_omtrent = 0,50. For en vegg brettet som i forrige eksempel: R_med = 3.65.
4. Q_n = 12 × 40 / 3,12 = 154 watt. Q_omtrent = 3 × 40 / 0,50 = 240 watt. Q_med = 29,4 × 40 / 3,65 = 322 W.
5. Generelt varmetap av modellrommet gjennom konvolutten Q = Q_n + Q_omtrent + Q_med = 716 watt.

Beregning ved å bruke de ovennevnte formlene gir en god tilnærming, forutsatt at materialet oppfyller den angitte varmeledningsevnen og det ikke er noen feil som kan gjøres under konstruksjonen. Et problem kan også være aldring av materialer og strukturen i huset som helhet.

Typisk vegg- og takgeometri

De lineære parametrene (lengde og høyde) på konstruksjonen når du bestemmer varmetap blir vanligvis tatt i stedet for utvendig. Det vil si at ved beregning av varmeoverføring gjennom materialet blir det tatt kontakt med området for varm, ikke kald luft.

Tatt i betraktning den indre omkretsen, er det nødvendig å ta hensyn til tykkelsen på innvendige partisjoner. Den enkleste måten å gjøre dette på er i henhold til husets plan, som vanligvis brukes på papir med storstilt rutenett.

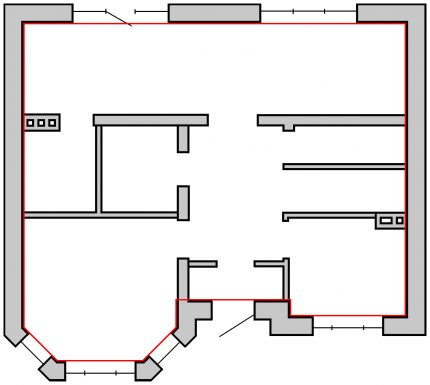
Således, for eksempel når dimensjonene til huset er 8 × 10 meter og veggtykkelsen er 0,3 meter, er den indre omkretsen P_vnut = (9,4 + 7,4) × 2 = 33,6 m, og den ytre P_ekstern = (8 + 10) × 2 = 36 moh.

Grensesnittoverlappingen har vanligvis en tykkelse fra 0,20 til 0,30 m. Derfor vil høyden på to etasjer fra gulvet i den første til taket på den andre fra utsiden være lik H_ekstern = 2,7 + 0,2 + 2,7 = 5,6 m. Hvis du bare legger opp etterbehandlingshøyden, får du en lavere verdi: H_vnut = 2,7 + 2,7 = 5,4 m. Overflate mellom gulv, i motsetning til vegger, har ikke funksjonen til isolasjon, for beregninger er det derfor nødvendig å ta H_ekstern.

For to etasjers hus med dimensjoner på rundt 200 moh² forskjellen mellom veggenes område ute og ute er fra 6 til 9%. Tilsvarende, med hensyn til interne dimensjoner, tas de geometriske parametrene til taket og gulvene i betraktning.

Beregningen av veggområdet for enkle hytter i geometri er elementær, siden fragmentene består av rektangulære seksjoner og pedimenter på loftet og loftet.

Frontene til loftene og loftet har i de fleste tilfeller formen av en trekant eller en femkant symmetrisk vertikalt. Det er ganske enkelt å beregne området deres

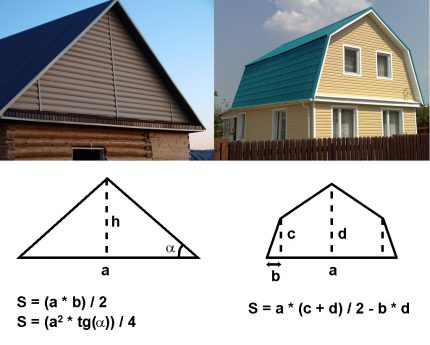
Når du beregner varmetap gjennom taket i de fleste tilfeller, er det nok å bruke formler for å finne områdene i en trekant, rektangel og trapes.

De mest populære takformene til private hus. Når du måler deres parametere, må det huskes at de indre dimensjonene er erstattet i beregningene (uten takskjegg)

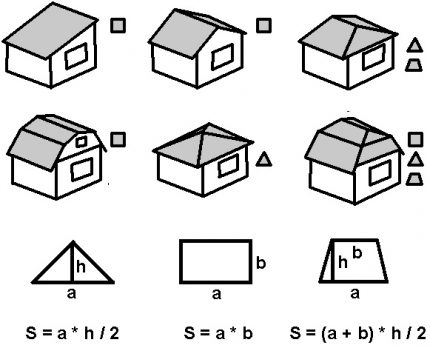
Arealet til det lagt taket kan ikke tas når du bestemmer varmetap, siden det også går til overheng som ikke er tatt hensyn til i formelen. I tillegg blir ofte materialet (for eksempel taktekking eller profilert galvanisert ark) plassert med en liten overlapping.

Noen ganger ser det ut til at det er ganske vanskelig å beregne takområdet. Imidlertid kan inne i huset geometrien til den isolerte gjerdingen i øverste etasje være mye enklere

Den rektangulære geometrien til vinduene skaper heller ikke problemer i beregningene. Hvis vinduer med doble vinduer har en sammensatt form, kan ikke arealet deres beregnes, men læres av produktpasset.

Varmetap gjennom gulv og grunnmur

Beregningen av varmetap til jorden gjennom gulvet i underetasjen, samt gjennom veggene og gulvet i kjelleren, vurderes i henhold til reglene foreskrevet i vedlegg "E" SP 50.13330.2012. Faktum er at frekvensen av varmeutbredelse i jorden er mye lavere enn i atmosfæren, derfor kan jord også betinget tilskrives isolasjonsmateriale.

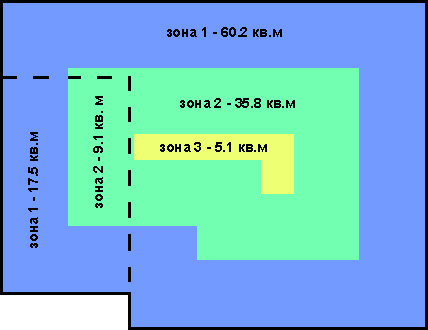
Men siden de er preget av frysing, er gulvet delt i 4 soner. Bredden på de tre første er 2 meter, og resten henvises til den fjerde.

Varmetapsonene i gulvet og kjelleren gjentar formen på fundamentets omkrets. Det viktigste varmetapet vil gå gjennom sone nr. 1

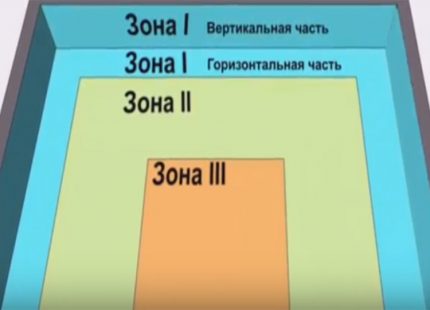
For hver sone må du bestemme koeffisienten for motstand mot varmeoverføring, som tilfører jord:

• sone 1: R₁ = 2.1;
• sone 2: R₂ = 4.3;
• sone 3: R₃ = 8.6;
• sone 4: R₄ = 14.2.

om gulvene er isolertfor deretter å bestemme den totale koeffisienten for termisk motstand legge opp indikatorene for isolasjon og jord.

Et eksempel. Anta at et hus med ytre dimensjoner på 10 × 8 m og en veggtykkelse på 0,3 meter har en kjeller med en dybde på 2,7 meter. Taket er plassert på bakkenivå. Det er nødvendig å beregne varmetapet til jorda ved en indre lufttemperatur på “+25 ° C” og en ekstern temperatur på “–15 ° C”.

La veggene være laget av FBS blokker 40 cm tykke (λ_f = 1,69). Innvendig er de trimmet med et brett som er 4 cm tykt (λ_d = 0,18). Kjelleretasjen helles med utvidet leirbetong, 12 cm tykk (λ_til = 0,70). Deretter koeffisienten for termisk motstand av veggene i kjelleren: R_med = 0,4 / 1,69 + 0,04 / 0,18 = 0,46, og gulvet R_n = 0.12 / 0.70 = 0.17.

Husets indre dimensjoner vil være 9,4 × 7,4 meter.

Opplegget med å dele kjelleren i soner for oppgaven. Beregningen av områder med så enkel geometri reduseres til å bestemme sidene på rektanglene og multiplikasjonen av dem

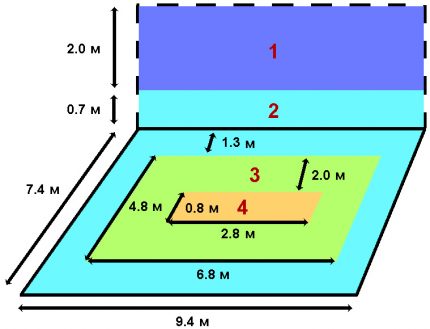
Vi beregner områdene og koeffisientene for motstand mot varmeoverføring ved soner:

• Sone 1 løper bare langs veggen. Den har en omkrets på 33,6 m og en høyde på 2 m. Derfor S₁ = 33.6 × 2 = 67.2. R_P1 = R_med + R₁ = 0.46 + 2.1 = 2.56.
• Sone 2 på veggen. Den har en omkrets på 33,6 m og en høyde på 0,7 m. Derfor S_2c = 33.6 × 0.7 = 23.52. R_z2s = R_med + R₂ = 0.46 + 4.3 = 4.76.
• Sone 2 på gulvet. S_2n = 9.4 × 7.4 – 6.8 × 4.8 = 36.92. R_z2p = R_n + R₂ = 0.17 + 4.3 = 4.47.
• Sone 3 er bare på gulvet. S₃ = 6.8 × 4.8 – 2.8 × 0.8 = 30.4. R_P3 = R_n + R₃ = 0.17 + 8.6 = 8.77.
• Sone 4 er bare på gulvet. S₄ = 2.8 × 0.8 = 2.24. R_P4 = R_n + R₄ = 0.17 + 14.2 = 14.37.

Første etasje varmetap Q = (S₁ / R_P1 + S_2c / R_z2s + S_2n / R_z2p + S₃ / R_P3 + S₄ / R_P4) × dT = (26,25 + 4,94 + 8,26 + 3,47 + 0,16) × 40 = 1723 W.

Regnskap for uoppvarmede lokaler

Ofte når man beregner varmetap, oppstår det en situasjon når huset har et uoppvarmet, men isolert rom. I dette tilfellet skjer energioverføring i to trinn. Vurder denne situasjonen på loftet.

På en varm, men ikke oppvarmet loft, i en kald periode, stilles temperaturen høyere enn på gaten. Dette skyldes overføring av varme gjennom gulvet.

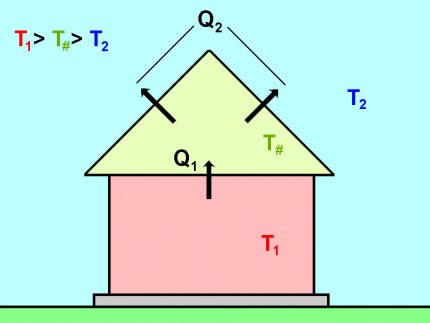
Hovedproblemet er at området med overlapping mellom loftet og øverste etasje er forskjellig fra området til taket og gavlene. I dette tilfellet er det nødvendig å bruke tilstanden for varmeoverføringsbalanse Q₁ = Q₂.

Det kan også skrives på følgende måte:

K₁ × (T₁ - T_#) = K₂ × (T_# - T₂),

der:

• K₁ = S₁ / R₁ + … + S_n / R_n for overlapping mellom den varme delen av huset og kjølerommet;
• K₂ = S₁ / R₁ + … + S_n / R_n for overlapping mellom et kjølerom og gaten.

Fra likhet med varmeoverføring finner vi temperaturen som vil bli etablert i et kjølerom med kjente verdier i huset og på gaten. T_# = (K₁ × T₁ + K₂ × T₂) / (K₁ + K₂). Etter det erstatter vi verdien i formelen og finner varmetapet.

Et eksempel. La husets indre størrelse være 8 x 10 meter. Takvinkelen er 30 °. Lufttemperaturen i rommene er “+25 ° С”, og utenfor “–15 ° С”.

Koeffisienten for termisk motstand i taket beregnes som i eksemplet gitt i seksjonen for beregning av varmetap gjennom bygningskonvolutter: R_n = 3,65. Overlappingsområdet er 80 moh²derfor K₁ = 80 / 3.65 = 21.92.

Takområdet S₁ = (10 × 8) / cos(30) = 92,38. Vi vurderer koeffisienten for termisk motstand, under hensyntagen til tykkelsen på treet (kasse og finish - 50 mm) og mineralull (10 cm): R₁ = 2.98.

Vinduområde for pediment S₂ = 1,5. For en vanlig to-kammer termisk motstand med dobbeltvinduer i vinduet R₂ = 0,4. Arealet av pedimentet beregnes med formelen: S₃ = 8² × tg(30) / 4 – S₂ = 7,74. Motstandskoeffisienten mot varmeoverføring er den samme som taket: R₃ = 2.98.

Varmeoverføring gjennom vinduer er en betydelig del av alt energitapet. I regioner med kalde vintre bør du derfor velge "varme" doble vinduer

Vi beregner koeffisienten for taket (ikke å glemme at antall pedimenter er to):

K₂ = S₁ / R₁ + 2 × (S₂ / R₂ + S₃ / R₃) = 92.38 / 2.98 + 2 × (1.5 / 0.4 + 7.74 / 2.98) = 43.69.

Vi beregner lufttemperaturen på loftet:

T_# = (21,92 × 25 + 43,69 × (–15)) / (21,92 + 43,69) = –1.64 ° С.

Vi erstatter den oppnådde verdien i en av formlene for å beregne varmetap (hvis de er balanserte, er de like) og vi oppnår ønsket resultat:

Q₁ = K₁ × (T₁ – T_#) = 21,92 × (25 - (–1.64)) = 584 W.

Ventilasjonskjøling

Et ventilasjonssystem er installert for å opprettholde et normalt mikroklima i huset. Dette fører til en tilstrømning av kald luft inn i rommet, som også må tas med i beregningen når man beregner varmetap.

Krav til ventilasjonsmengde er stavet ut i flere forskriftsdokumenter. Når man utformer et internt hyttesystem, må man først og fremst ta hensyn til kravene i §7 SNiP 41-01-2003 og §4 SanPiN 2.1.2.2645-10.

Siden watt er den generelt aksepterte enheten for å måle varmetap, er luftens varmekapasitet c (kJ / kg × ° C) må reduseres til dimensjonen “W × h / kg × ° C”. For luft på havnivå kan du ta verdien c = 0,28 W × h / kg × ° C.

Siden ventilasjonsvolumet måles i kubikk i timen, er det også nødvendig å kjenne lufttettheten q (kg / m³). Ved normalt atmosfæretrykk og gjennomsnittlig luftfuktighet kan denne verdien tas = 1,30 kg / m³.

Husholdningsventilasjonsenhet med recuperator. Det deklarerte volumet som den går glipp av, blir gitt med en liten feil. Derfor er det ikke fornuftig å nøyaktig beregne tettheten og varmekapasiteten til luft i området opp til hundredeler

Energiforbruket for kompensasjon av varmetap på grunn av ventilasjon kan beregnes ved hjelp av følgende formel:

Q = L × q × c × dT = 0,364 × L × dT,

der:

• L - luftforbruk (m³ / h);
• dT - temperaturforskjell mellom rom og innkommende luft (° C).

Hvis kald luft kommer direkte inn i huset, så:

dT = T₁ - T₂,

der:

• T₁ - innetemperatur;
• T₂ - temperatur ute.

Men for store gjenstander i ventilasjonssystemet vanligvis integrere recuperator (varmeveksler). Det kan spare energi betydelig, da delvis oppvarming av den innkommende luften skjer på grunn av utløpsstrømmen.

Effektiviteten til slike enheter måles i effektiviteten k (%). I dette tilfellet vil den forrige formelen ha formen:

dT = (T₁ - T₂) × (1 - k / 100).

Beregning av gasstrøm

vite totalt varmetap, kan du bare beregne det nødvendige forbruket av naturlig eller flytende gass for oppvarming av et hus med et areal på 200 meter².

Mengden energi som frigjøres, i tillegg til drivstoffvolumet, påvirkes av dens brennverdi. For gass avhenger denne indikatoren av fuktighet og kjemisk sammensetning av den tilførte blandingen. Skill den høyeste (H_h) og lavere (H_l) brennverdi.

Den lavere brennverdien av propan er mindre enn for butan. Derfor, for å nøyaktig bestemme brennverdien av flytende gass, må du vite prosentandelen av disse komponentene i blandingen som leveres til kjelen

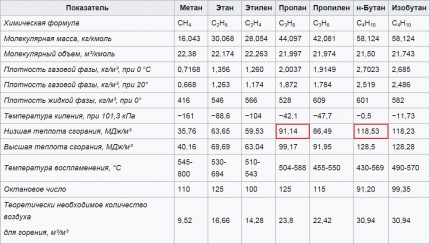
For å beregne mengden drivstoff som garantert er tilstrekkelig til oppvarming, erstattes den lavere brennverdien, som kan fås fra gassleverandøren, i formelen. Standardenheten for brennverdi er “mJ / m³”Eller“ mJ / kg ”. Men siden måleenhetene og effekten til kjelene og varmetapene fungerer med watt, ikke joules, er det nødvendig å utføre konverteringen, gitt 1 mJ = 278 W × h.

Hvis verdien av blandingens lavere brennverdi er ukjent, er det tillatt å ta følgende gjennomsnittlige tall:

• for naturgass H_l = 9,3 kW × h / m³;
• for flytende gass H_l = 12,6 kW × t / kg.

En annen indikator som er nødvendig for beregninger er kjelens effektivitet K. Vanligvis måles det i prosent. Den endelige formelen for gasstrøm over en periode E (h) har følgende skjema:

V = Q × E / (H_l × K / 100).

Perioden når sentralvarme i hus slås på, bestemmes av den gjennomsnittlige daglige lufttemperaturen.

Hvis det i løpet av de siste fem dagene ikke har overskredet "+ 8 ° С", må det i henhold til dekret fra Russlands føderasjon nr. 307 datert 05/13/2006 leveres varmeforsyning til huset. For private hjem med autonom oppvarming brukes disse tallene også ved beregning av drivstofforbruk.

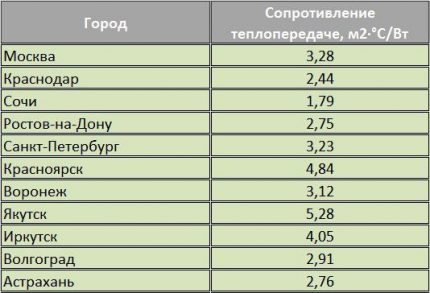
De nøyaktige dataene om antall dager med en temperatur ikke høyere enn “+ 8 ° С” for området der hytta er bygd, finner du i den lokale grenen til Hydrometeorological Center.

Hvis huset ligger nær et stort bebyggelse, er det lettere å bruke bordet. 1. SNiP 23-01-99 (kolonne nr. 11). Ved å multiplisere denne verdien med 24 (timer per dag) får vi parameteren E fra ligningen for beregning av gasstrøm.

I følge klimadata fra tabellen. 1 SNiP 23-01-99, blir beregninger utført av anleggsorganisasjoner for å bestemme varmetap for bygninger

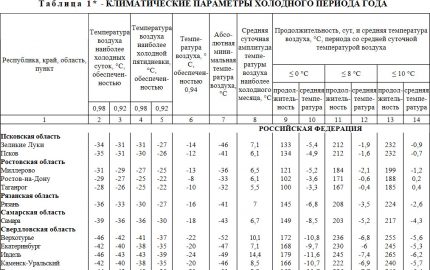
Hvis volumet av luftinnstrømning og temperaturen i rommene er konstant (eller med svake svingninger), vil varmetapet gjennom bygningskonvolutten og på grunn av ventilasjonen i rommene være direkte proporsjonal med utetemperaturen.

Derfor per parameter T₂ i ligningene for beregning av varmetap kan du ta verdien fra kolonne nr. 12 i tabellen. 1. SNiP 23-01-99.

Eksempel på en 200 m hytte²

Vi beregner gassforbruket for en hytte i nærheten av byen Rostov-på-Don. Varighet av oppvarmingsperiode: E = 171 × 24 = 4104 t. Gjennomsnittlig gatetemperatur T₂ = - 0,6 ° C. Ønsket temperatur i huset: T₁ = 24 ° C.

To-etasjes hytte med uoppvarmet garasje. Det totale arealet er ca 200 m2. Veggene er ikke i tillegg isolert, noe som er akseptabelt for klimaet i Rostov-regionen

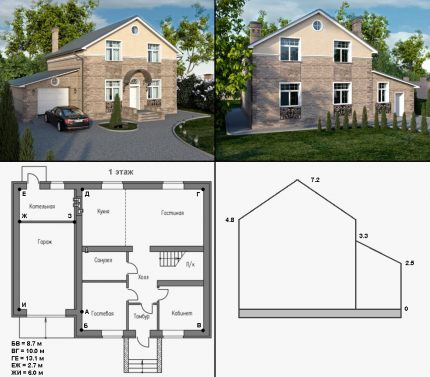
Trinn 1 Vi beregner varmetapet gjennom omkretsen uten å ta hensyn til garasjen.

For å gjøre dette, velg homogene seksjoner:

• Vinduene. Totalt er det 9 vinduer 1,6 × 1,8 m i størrelse, ett vindu 1,0 × 1,8 m i størrelse og 2,5 runde vinduer 0,38 m i størrelse² hver og en. Totalt vinduområde: S_vinduer = 28,60 moh². I følge passet av produkter R_vinduer = 0,55. deretter Q_vinduer = 1279 watt.
• Door. Det er 2 isolerte dører som måler 0,9 x 2,0 m. Området deres: S_døren = 3,6 moh². I følge produktpasset R_døren = 1,45. deretter Q_døren = 61 watt.
• Tom vegg. Seksjon “ABVGD”: 36,1 × 4,8 = 173,28 moh². Tomt “JA”: 8,7 × 1,5 = 13,05 moh². Plott “DEJ”: 18,06 moh². Arealet av takvelgen: 8,7 × 5,4 / 2 = 23,49. Totalt tomt veggområde: S_veggen = 251.37 – S_vinduer – S_døren = 219,17 moh². Veggene er laget av luftbetong 40 cm tykk og hulvendt murstein. R_veggene = 2,50 + 0,63 = 3,13. deretter Q_veggene = 1723 W.

Totalt varmetap gjennom omkretsen:

Q_Perim = Q_vinduer + Q_døren + Q_veggene = 3063 watt

Trinn 2 Vi beregner varmetapet gjennom taket.

Isolasjonen er en kontinuerlig kasse (35 mm), mineralull (10 cm) og fôr (15 mm). R_taket = 2,98. Takareal over hovedbygningen: 2 × 10 × 5,55 = 111 moh²og over kjelerommet: 2,7 × 4,47 = 12,07 moh². totalt S_taket = 123,07 moh². deretter Q_taket = 1016 watt.

Trinn 3 Beregn varmetap gjennom gulvet.

Arealene for det oppvarmede rommet og garasjen må beregnes separat. Området kan bestemmes nøyaktig med matematiske formler, eller det kan også gjøres ved hjelp av vektorredigerere som Corel Draw

Motstand mot varmeoverføring tilveiebringes av brettene i det grove gulvet og kryssfiner under laminatet (5 cm totalt), samt basaltisolering (5 cm). R_kjønn = 1,72. Da vil varmetapet gjennom gulvet være lik:

Q_etasje = (S₁ / (R_etasje + 2.1) + S₂ / (R_etasje + 4.3) + S₃ / (R_etasje + 2.1)) × dT = 546 watt.

Trinn 4 Vi beregner varmetapet gjennom en kald garasje. Gulvet er ikke isolert.

Fra et oppvarmet hus trenger varme på to måter:

1. Gjennom bæreveggen. S₁ = 28.71, R₁ = 3.13.
2. Gjennom en murvegg med et fyrrom. S₂ = 11.31, R₂ = 0.89.

Vi får K₁ = S₁ / R₁ + S₂ / R₂ = 21.88.

Fra garasjen går varmen ut som følger:

1. Gjennom vinduet. S₁ = 0.38, R₁ = 0.55.
2. Gjennom porten. S₂ = 6.25, R₂ = 1.05.
3. Gjennom veggen. S₃ = 19.68, R₃ = 3.13.
4. Gjennom taket. S₄ = 23.89, R₄ = 2.98.
5. Over hele gulvet. Sone 1. S₅ = 17.50, R₅ = 2.1.
6. Over hele gulvet. Sone 2. S₆ = 9.10, R₆ = 4.3.

Vi får K₂ = S₁ / R₁ + … + S₆ / R₆ = 31.40

Vi beregner temperaturen i garasjen, med forbehold om balansen i varmeoverføring: T_# = 9,2 ° C. Da vil varmetapet være lik: Q_garasjen = 324 watt.

Trinn 5 Vi beregner varmetapet på grunn av ventilasjon.

La det beregnede ventilasjonsvolumet for en slik hytte med 6 personer som bor der være 440 moh³/ time En recuperator med en effektivitet på 50% er installert i systemet. Under disse forholdene, varmetap: Q_vent = 1970 watt

Trinn. 6. Vi bestemmer det totale varmetapet ved å legge til alle lokale verdier: Q = 6919 watt

Trinn 7 Vi beregner mengden gass som trengs for å varme opp modellhuset om vinteren med en kjeleeffektivitet på 92%:

• Naturgass. V = 3319 moh³.
• Flytende gass. V = 2450 kg.

Etter beregninger kan du analysere de økonomiske kostnadene ved oppvarming og gjennomførbarheten av investeringer som har som mål å redusere varmetapet.

Konklusjoner og nyttig video om emnet

Varme ledningsevne og varmeoverføringsmotstand av materialer. Beregningsregler for vegger, tak og gulv:

Den vanskeligste delen av beregningene for å bestemme volumet av gass som trengs for oppvarming, er å finne varmetapet til den oppvarmede gjenstanden. Her må du først og fremst vurdere geometriske beregninger nøye.

Hvis de økonomiske kostnadene ved oppvarming virker for høye, bør du tenke på ytterligere isolering av huset. Videre viser beregninger av varmetap godt frysestrukturen.

Legg igjen kommentarer i blokken nedenfor, still spørsmål om uklare og interessante punkter, legg ut et bilde om emnet for artikkelen. Del din egen erfaring med å lage beregninger for å finne ut kostnadene ved oppvarming. Det er mulig at rådene dine vil hjelpe besøkende på nettstedet.