Ohmin laki koko ketjulle ja ketjun osalle: kaavojen kirjoittaminen, kuvaus ja selitys
Ammattimainen sähköasentaja, erikoistunut elektroniikkainsinööri ei voi kiertää Ohmin lakia omassa toiminnassaan ratkaisemalla ongelmia, jotka liittyvät sähköisten ja sähköisten piirien asettamiseen, virittämiseen, korjaamiseen.
Itse asiassa jokainen tarvitsee ymmärtää tätä lakia. Koska jokaisen jokapäiväisessä elämässä on käsiteltävä sähköä.
Ja vaikka saksalaisen fyysikon Ohmin laista säädetään lukion kurssilla, sitä ei käytännössä aina opitata ajoissa. Siksi harkitsemme materiaalissamme sellaista elämää koskevaa aihetta ja käsittelemme kaavan kirjoittamisen vaihtoehtoja.
Artikkelin sisältö:
Erillinen osa ja täydellinen sähköpiiri
Kun tarkastellaan sähköpiiriä Ohmin lain soveltamisen kannalta piiriin, on huomioitava kaksi mahdollista laskentavaihtoehtoa: yhdelle osalle ja täysimittaiselle piirille.
Sähköpiirin virtaosan laskeminen
Piirin osaa, pääsääntöisesti, pidetään piirin osana, pois lukien EMF-lähteen, jolla on ylimääräinen sisäinen vastus.
Siksi laskentakaava näyttää tässä tapauksessa yksinkertaiselta:
I = U / R,
Missä vastaavasti:
- minä - virran lujuus;
- U - käytetty jännite;
- R - vastus.
Kaavan tulkinta on yksinkertainen - tiettyä piirin osaa pitkin virtaava virta on verrannollinen siihen kohdistettuun jännitteeseen, ja vastus on kääntäen verrannollinen.
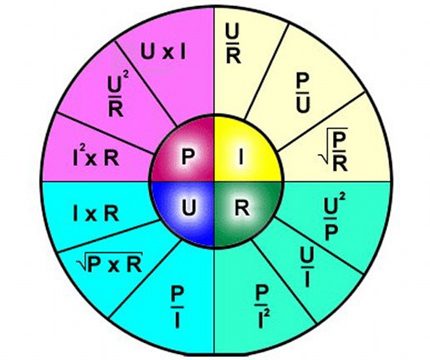
Siten kaava kuvaa selvästi sähköpiirin erillisen osan läpi virtaavan virran riippuvuuden tietyistä jännitteen ja vastuksen arvoista.
On mukavaa käyttää kaavaa esimerkiksi laskettaessa vastusparametreja, jotka on juotettava piiriin, jos jännite virralla on määritelty.
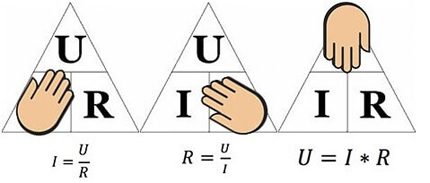
Yllä oleva kuva auttaa määrittämään esimerkiksi virran, joka virtaa 10 ohmin vastuksen läpi, johon kohdistetaan 12 voltin jännite. Korvaavat arvot, löydämme - I = 12/10 = 1,2 ampeeria.
Samalla tavoin ratkaistaan vastuksen (kun virta jännitteellä tunnetaan) tai jännitteen (kun jännite virralla tunnetaan) löytämisen tehtävät.
Siksi on aina mahdollista valita tarvittava käyttöjännite, vaadittava ampeeri ja optimaalinen resistiivinen elementti.
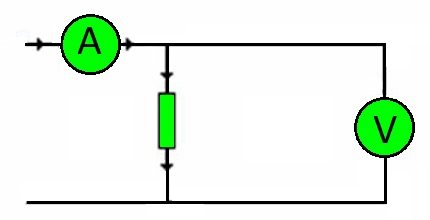
Muuten, minkä tahansa piirin kytkentäjohdot ovat vastus. Kuorman suuruus, joka heidän on kannettava, määräytyy jännitteen perusteella.
Vastaavasti jälleen Ohmin lakia käyttämällä on mahdollista valita tarkkaan tarvittava johtimen poikkileikkaus ytimen materiaalista riippuen.
Meillä on yksityiskohtaiset ohjeet verkkosivustolla kaapelin poikkileikkaus voimalla ja virralla.
Koko ketjun laskentavaihtoehto
Koko ketju on jo paikka (alueet), samoin kuin EMF: n lähde. Toisin sanoen EMF-lähteen sisäinen resistanssi lisätään piiriosan olemassa olevaan resistiiviseen komponenttiin.
Siksi jotkut muutokset yllä olevaan kaavaan ovat loogisia:
I = U / (R + r)
EMM: n sisäisen resistanssin arvoa Ohmin laissa täydelliselle sähköpiirille voidaan tietysti pitää vähäpätöisenä, vaikkakin tämä vastusarvo riippuu monessa suhteessa EMF-lähteen rakenteesta.
Laskettaessa monimutkaisia elektronisia piirejä, sähköjohtoja, joissa on monia johtimia, lisävastuksen esiintyminen on tärkeä tekijä.
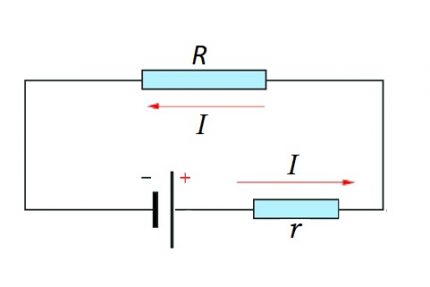
Sekä piiriosassa että koko piirissä tulee ottaa huomioon luonnollinen momentti - vakio- tai muuttuvan virran käyttö.
Jos yllä mainittuja Ohmin laille ominaisia kohtia otettaisiin huomioon tasavirran käytön kannalta, vastaavasti vaihtovirralla kaikki näyttää hieman erilaiselta.
Lain huomioon ottaminen muuttujalle
Käsitettä "vastus" vaihtovirran kulkuedellytyksille olisi pidettävä enemmän "impedanssin" käsitteenä. Tämä on aktiivisen resistiivisen kuorman (Ra) ja reaktiivisen vastuksen (Rr) muodostaman kuorman yhdistelmä.
Tällaisia ilmiöitä aiheuttavat induktiivisten elementtien parametrit ja kytkentälait, joita sovelletaan muuttuvaan jännitearvoon - sinimuotoiseen virta-arvoon.
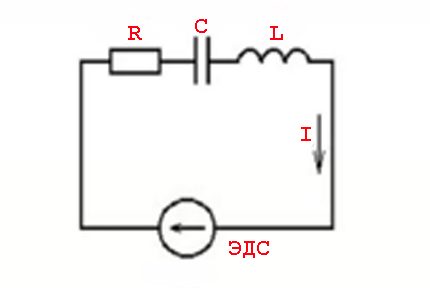
Toisin sanoen, virta-arvojen siirtämisellä (viiveellä) jännitearvoista on seurausta, jota seuraa aktiivisten (resistiivisten) ja reaktiivisten (induktiivisten tai kapasitiivisten) kapasiteettien esiintyminen.
Tällaisten ilmiöiden laskenta tapahtuu kaavalla:
Z = U / I tai Z = R + J * (XL - XC)
missä: Z - impedanssi; R - aktiivinen kuorma; XL , XC - induktiivinen ja kapasitiivinen kuorma; J - kerroin.
Elementtien sarja ja rinnankytkentä
Sähköpiirin (piiriosan) elementteille ominaismomentti on sarja- tai rinnakkaisliitäntä.
Vastaavasti jokaiselle kytkentätyypille seuraa virran virtauksen ja jännitesyötön erilainen luonne. Tässä suhteessa Ohmin lakia sovelletaan myös eri tavoin, riippuen mahdollisuudesta sisällyttää elementtejä.
Vastuspiiri
Sarjayhteyteen (piirin osa, jossa on kaksi komponenttia) käytetään seuraavaa kaavaa:
- I = i1 = Minä2 ;
- U = U1 + U2 ;
- R = R1 + R2
Tämä formulaatio osoittaa selvästi, että riippumatta sarjaan kytkettyjen resistiivisten komponenttien lukumäärästä, piirissä virtaava virta ei muutu.
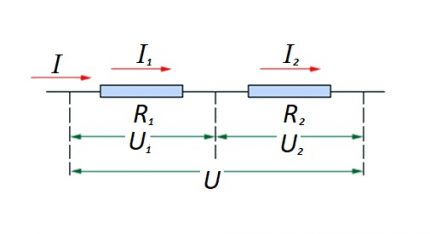
Piirin aktiivisiin resistiivisiin komponentteihin kohdistetun jännitteen suuruus on emf-lähteen kokonaisarvon summa.
Kunkin yksittäisen komponentin jännite on yhtä suuri kuin: Ux = I * Rx.
Kokonaisvastusta tulisi pitää piirin kaikkien resistiivisten komponenttien nimellisarvojen summana.
Rinnakkain kytkettyjen resistiivisten elementtien piiri
Tapauksissa, joissa resistiiviset komponentit on kytketty rinnakkain, seuraavaa kaavaa pidetään oikeudenmukaisena saksalaisen fyysikon Ohmin lain suhteen:
- I = i1 + Minä2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Vaihtoehtoja sekoitetun piirilevyjen kokoamiseksi, kun käytetään rinnakkais- ja sarjayhteyttä, ei ole suljettu pois.
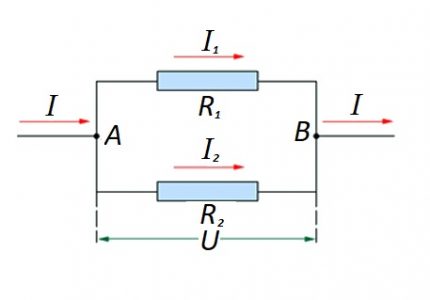
Tällaisille vaihtoehdoille laskenta suoritetaan yleensä laskemalla rinnakkaisliitännän resistiivinen nimellisarvo. Sitten sarjaan kytketyn vastuksen arvo lisätään tulokseen.
Integraaliset ja erilaiset laki
Kaikki edellä mainitut laskelmien kohdat ovat sovellettavissa olosuhteisiin, joissa sähköpiireissä käytetään "homogeenisen" rakenteen johtimia.
Samaan aikaan käytännössä joudutaan usein käsittelemään piirin rakentamista, jossa johtimien rakenne muuttuu eri alueilla. Esimerkiksi käytetään suurempien poikkipinta-alan lankoja tai päinvastoin pienempiä lankoja, jotka on valmistettu eri materiaaleista.
Tällaisten erojen huomioon ottamiseksi on olemassa variaatio ns. "Ohmin differentiaalintegraalilaista". Äärimmäisen pienelle johtimelle virtatiheysaste lasketaan lujuudesta ja johtavuudesta riippuen.
Erotuslaskelmassa käytetään kaavaa: J = ό * E
Kokonaislaskelmaa varten vastaavasti: I * R = φ1 - φ2 + έ
Nämä esimerkit ovat kuitenkin melko lähempänä korkea-asteen matematiikan koulua, ja käytännössä yksinkertaista sähköasentajaa ei todellakaan käytetä.
Päätelmät ja hyödyllinen video aiheesta
Yksityiskohtainen analyysi Ohmin laista alla olevassa videossa auttaa lopullisesti vakiinnuttamaan tietämystä tähän suuntaan.
Erityinen videotunti vahvistaa kvalitatiivisesti teoreettista kirjallista esitystä:
Sähköasentajan työ tai sähköinsinöörin toiminta liittyy erottamattomasti hetkiin, jolloin sinun on todella noudatettava Georg Ohmin lakia toiminnassa. Nämä ovat joitain yleisiä totuuksia, jotka jokaisen ammattilaisen tulisi tietää.
Laajaa tietoa tästä aiheesta ei vaadita - riittää, kun opitaan sanamuodon kolme päämuotoa, jotta sitä voidaan soveltaa käytännössä.
Haluatko täydentää yllä olevaa materiaalia arvokkaiin kommentteihin tai ilmaista mielipiteesi? Kirjoita kommentit artikkelin alapuolelle. Jos sinulla on kysyttävää, kysy rohkeasti asiantuntijoitamme.

 Kuinka laskea teho, virta ja jännite: periaatteet ja esimerkit laskennasta kotimaisille olosuhteille
Kuinka laskea teho, virta ja jännite: periaatteet ja esimerkit laskennasta kotimaisille olosuhteille  Ampeerien muuntaminen watteiksi: säännöt ja käytännön esimerkit jännite- ja virtayksiköiden muuntamisesta
Ampeerien muuntaminen watteiksi: säännöt ja käytännön esimerkit jännite- ja virtayksiköiden muuntamisesta  Kuinka muuntaa ampeereita kilowatteiksi: käännösperiaatteet ja käytännön esimerkit selityksineen
Kuinka muuntaa ampeereita kilowatteiksi: käännösperiaatteet ja käytännön esimerkit selityksineen  Keskeytymätön tietokoneelle: parhaan UPS: n luokitus
Keskeytymätön tietokoneelle: parhaan UPS: n luokitus  Sähköpiirien käytännöt: grafiikan ja aakkosnumeeristen merkkien dekoodaus
Sähköpiirien käytännöt: grafiikan ja aakkosnumeeristen merkkien dekoodaus  Muunna kilowatit hevosvoimaan: kuinka monta lääkettä yhdessä kW + periaatteet ja laskentatavat
Muunna kilowatit hevosvoimaan: kuinka monta lääkettä yhdessä kW + periaatteet ja laskentatavat  Kuinka paljon kaasun kytkeminen omakotitaloon maksaa: kaasuntoimituksen järjestämisen hinta
Kuinka paljon kaasun kytkeminen omakotitaloon maksaa: kaasuntoimituksen järjestämisen hinta  Parhaat kuivausrummulla varustetut pesukoneet: malliluokitus ja asiakasvinkit
Parhaat kuivausrummulla varustetut pesukoneet: malliluokitus ja asiakasvinkit  Mikä on valon värilämpötila ja miten valon lamppujen lämpötila valitaan tarpeitasi vastaavasti?
Mikä on valon värilämpötila ja miten valon lamppujen lämpötila valitaan tarpeitasi vastaavasti?  Geyserin vaihtaminen asunnossa: korvaava paperityö + perusnormit ja vaatimukset
Geyserin vaihtaminen asunnossa: korvaava paperityö + perusnormit ja vaatimukset