חוק אוהם לשרשרת השלמה ולגזרת השרשרת: כתיבת נוסחאות, תיאור והסבר
חשמלאי מקצועי, מהנדס אלקטרוניקה מומחה לא יכול לעקוף את חוק אוהם בפעילויותיו שלו, ולפתור בעיות הקשורות בהקמה, כוונון, תיקון מעגלים אלקטרוניים וחשמליים.
למעשה, כולם זקוקים להבנה של החוק הזה. כי כל אחד בחיי היומיום צריך להתמודד עם חשמל.
ואף על פי שחוק הפיזיקאי הגרמני אוהם נקבע על ידי קורס בתיכון תיכוניים, בפועל הוא לא תמיד נלמד בצורה מתוזמנת. לכן נשקול בחומר שלנו נושא כזה שרלוונטי לכל החיים ונעסוק באפשרויות לכתיבת הנוסחה.
תוכן המאמר:
קטע נפרד ומעגל חשמל מלא
בהתחשב במעגל החשמלי מנקודת המבט של החלת החוק של אוהם על המעגל, יש לציין שתי אפשרויות חישוב אפשריות: לקטע בודד ולמעגל מן המניין.
חישוב החלק הנוכחי של מעגל החשמל
החלק של המעגל, ככלל, נחשב לחלק מהמעגל, למעט מקור ה- EMF, כבעל התנגדות פנימית נוספת.
לכן, נוסחת החישוב, במקרה זה, נראית פשוטה:
I = U / R,
איפה, בהתאמה:
- אני - חוזק זרם;
- U - מתח מוחל;
- ר - התנגדות.
הפרשנות של הנוסחה היא פשוטה - הזרם שזורם בחלק מסוים של המעגל הוא פרופורציונלי למתח המופעל עליו, וההתנגדות היא פרופורציונית הפוכה.
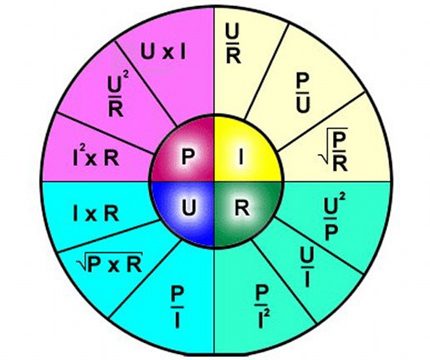
לפיכך, הנוסחה מתארת בבירור את התלות של הזרם הזורם בקטע נפרד של המעגל החשמלי ביחס לערכים מסוימים של מתח והתנגדות.
נוח להשתמש בנוסחה, למשל, בחישוב פרמטרי ההתנגדות, אותם יש להלחם במעגל אם מוגדר המתח עם הזרם.
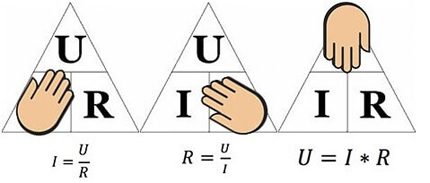
הנתון לעיל יסייע לקבוע, למשל, את הזרם הזורם בהתנגדות של 10 אוהם, אליו מופעל מתח של 12 וולט. אנו מחליפים את החלפת הערכים - I = 12/10 = 1.2 אמפר.
באופן דומה, נפתרות המשימות של מציאת התנגדות (כאשר ידועים זרם עם מתח) או מתח (כאשר ידועים מתח עם זרם).
כך, תמיד ניתן לבחור את מתח ההפעלה הנדרש, את הקוטר הנדרש ואת אלמנט ההתנגדות האופטימלי.
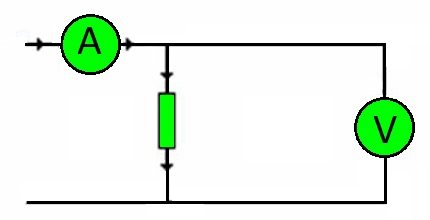
אגב, חוטי החיבור של כל מעגל הם התנגדות. גודל העומס שהם צריכים לשאת נקבע על ידי המתח.
בהתאם, שוב באמצעות החוק של אוהם, ניתן לבחור במדויק את חתך המוליך הדרוש, תלוי בחומר הליבה.
יש לנו הוראות מפורטות באתר חתך כבל על ידי כוח וזרם.
אפשרות חישוב לשרשרת מלאה
שרשרת שלמה היא כבר האתר (ים), כמו גם מקור ה- EMF. כלומר, למעשה, ההתנגדות הפנימית של מקור ה- EMF מתווספת לרכיב ההתנגדות הקיים בקטע המעגל.
לכן שינוי מסוים בנוסחה הנ"ל הוא הגיוני:
I = U / (R + r)
כמובן שערך ההתנגדות הפנימית של EMF בחוקיו של אוהם למעגל חשמלי שלם יכול להיחשב זניח, אם כי במובנים רבים ערך ההתנגדות הזה תלוי במבנה המקור של EMF.
עם זאת, בעת חישוב מעגלים אלקטרוניים מורכבים, מעגלים חשמליים עם מוליכים רבים, נוכחות של התנגדות נוספת היא גורם חשוב.
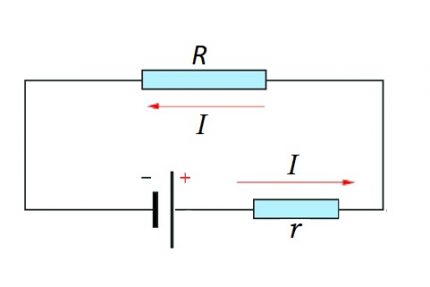
הן עבור מקטע המעגל והן עבור המעגל השלם, יש לקחת בחשבון את הרגע הטבעי - שימוש בזרם קבוע או משתנה.
אם הנקודות שצוינו לעיל, האופייניות לחוקיו של אוהם, נחשבו מנקודת המבט של שימוש בזרם ישר, בהתאם לזרם חילופין הכל נראה מעט שונה.
התחשבות בחוק למשתנה
יש לראות במושג "התנגדות" לתנאי מעבר זרם חילופין יותר כמושג "עכבה". זהו שילוב של העומס ההתנגדי הפעיל (Ra) והעומס שנוצר על ידי הנגד התגובה (Rr).
תופעות כאלה נגרמות על ידי הפרמטרים של אלמנטים אינדוקטיביים וחוקי המיתוג כפי שהם חלים על ערך מתח משתנה - ערך זרם סינוסואידי.
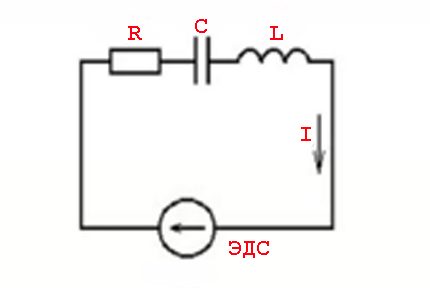
במילים אחרות, ישנה השפעה של קידום (מפגר) של ערכי זרם מערכי מתח, המלווה במראה של יכולות פעילות (התנגדות) ותגובות (אינדוקטיביות או קיבוליות).
חישוב תופעות כאלה מתבצע באמצעות הנוסחה:
Z = U / I או Z = R + J * (Xל - Xג)
איפה: ז - עכבה; ר - עומס פעיל; Xל , Xג - עומס אינדוקטיבי וקיבולי; ג - מקדם.
סדרה וחיבור מקביל של אלמנטים
עבור אלמנטים של מעגל חשמלי (קטע מעגל), רגע אופייני הוא סדרה או חיבור מקביל.
בהתאם, כל סוג של חיבור מלווה באופי שונה של הזרם ואספקת המתח. בעניין זה החוק של אוהם חל גם בדרכים שונות, תלוי באפשרות לכלול יסודות.
מעגל נגד
ביחס לחיבור סדרתי (קטע במעגל עם שני רכיבים), הנוסחה הבאה משמשת:
- אני = אני1 = אני2 ;
- U = U1 + U2 ;
- R = R1 + R2
ניסוח זה ממחיש בבירור כי ללא קשר למספר הרכיבים ההתנגדים המחוברים בסדרה, הזרם הזורם במעגל אינו משתנה.
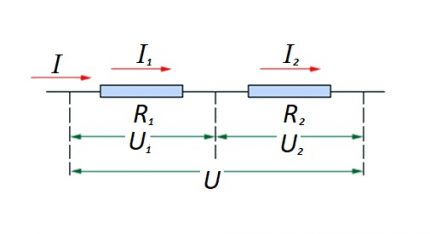
גודל המתח המופעל על רכיבי ההתנגדות הפעילים במעגל הוא סכום הערך הכולל של מקור ה- emk.
המתח על כל רכיב בודד שווה ל: Ux = I * Rx.
יש להתייחס להתנגדות הכוללת כאל סכום הדירוגים של כל המרכיבים ההתנגדים במעגל.
מעגל של רכיבי התנגדות מקבילים מחוברים
במקרה שיש קשר מקביל של רכיבים התנגדים, הנוסחה הבאה נחשבת הוגנת ביחס לחוקו של הפיזיקאי הגרמני אוהם:
- אני = אני1 + אני2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
אין לשלול אפשרויות להרכבת קטעי מעגלים מסוג "מעורב" בעת שימוש בחיבור מקבילי וטורי.
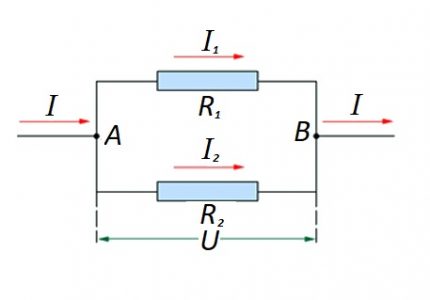
עבור אפשרויות כאלה, החישוב מתבצע בדרך כלל על ידי החישוב הראשוני של הדירוג ההתנגד של החיבור המקביל. לאחר מכן, ערך הנגד המחובר בסדרה מתווסף לתוצאה.
צורות משפט אינטגרליות ודיפרנציאליות
כל הנקודות לעיל עם החישובים חלות על תנאים בהם משתמשים במוליכים עם מבנה "הומוגני" במעגלי החשמל.
בינתיים, בפועל, לעתים קרובות יש להתמודד עם בניית מעגל בו מבנה המוליכים משתנה באזורים שונים. לדוגמה, משתמשים בחוטים בעלי חתך גדול יותר או להפך, קטנים יותר, המיוצרים על בסיס חומרים שונים.
כדי להסביר את ההבדלים הללו, יש וריאציה של מה שמכונה "החוק ההבדל-אינטגרלי של אוהם". עבור מוליך קטן עד אינסוף, רמת הצפיפות הנוכחית מחושבת בהתאם לחוזק והמוליכות.
תחת החישוב ההפרש, הנוסחה נלקחת: J = ό * ה
לחישוב אינטגרלי, בהתאמה, הנוסח: I * R = φ1 - φ2 + έ
עם זאת, דוגמאות אלה קרובות יותר לבית הספר למתמטיקה גבוהה יותר ובאימון בפועל, חשמלאי פשוט אינו משמש למעשה.
מסקנות ווידאו שימושי בנושא
ניתוח מפורט של החוק של אוהם בסרטון שלהלן יעזור לגבש סופית את הידע בכיוון זה.
שיעור וידיאו משונה מחזק באופן איכותי את המצגת הכתובה התיאורטית:
עבודתו של חשמלאי או פעילותו של מהנדס אלקטרוניקה קשורים זה בזה באופן בלתי נפרד לרגעים שבהם באמת צריך לשמור על החוק של גאורג אוהם בפעולה. אלה כמה אמיתות שכיחות שכל איש מקצוע צריך לדעת.
אין צורך בידע נרחב בנושא זה - די ללמוד את שלוש הווריאציות העיקריות של הנוסח כדי ליישם בהצלחה בפועל.
האם ברצונך להוסיף את החומר לעיל בתגובות יקרות ערך או להביע את דעתך? אנא כתוב הערות בבלוק שמתחת למאמר. אם יש לך שאלות, אל תהסס לשאול את המומחים שלנו.

 כיצד לחשב כוח, זרם ומתח: עקרונות ודוגמאות לחישוב לתנאים ביתיים
כיצד לחשב כוח, זרם ומתח: עקרונות ודוגמאות לחישוב לתנאים ביתיים  המרת אמפר לוואטים: כללים ודוגמאות מעשיות להמרת יחידות מתח וזרם
המרת אמפר לוואטים: כללים ודוגמאות מעשיות להמרת יחידות מתח וזרם  כיצד להמיר אמפר לקילוואט: עקרונות של תרגום ודוגמאות מעשיות עם הסברים
כיצד להמיר אמפר לקילוואט: עקרונות של תרגום ודוגמאות מעשיות עם הסברים  ללא הפרעה למחשב: דירוג של ה- UPS הטוב ביותר
ללא הפרעה למחשב: דירוג של ה- UPS הטוב ביותר  מוסכמות במעגלים חשמליים: פענוח גרפיקה ותווים אלפאנומריים
מוסכמות במעגלים חשמליים: פענוח גרפיקה ותווים אלפאנומריים  המר קילוואט לכוח סוס: כמה תרופות בכיס אחת + עקרונות ושיטות חישוב
המר קילוואט לכוח סוס: כמה תרופות בכיס אחת + עקרונות ושיטות חישוב  כמה עולה לחבר גז לבית פרטי: מחיר ארגון אספקת הדלק
כמה עולה לחבר גז לבית פרטי: מחיר ארגון אספקת הדלק  מכונות הכביסה הטובות ביותר עם מייבש: דירוג הדגם וטיפים ללקוחות
מכונות הכביסה הטובות ביותר עם מייבש: דירוג הדגם וטיפים ללקוחות  מה טמפרטורת הצבע של האור והניואנסים של בחירת הטמפרטורה של המנורות בהתאם לצרכים שלך
מה טמפרטורת הצבע של האור והניואנסים של בחירת הטמפרטורה של המנורות בהתאם לצרכים שלך  החלפת גייזר בדירה: ניירת חלופית + נורמות ודרישות בסיסיות
החלפת גייזר בדירה: ניירת חלופית + נורמות ודרישות בסיסיות