Ohmas likums par visu ķēdi un tās daļu: formulas rakstīšana, apraksts un skaidrojums

Profesionāls elektriķis, speciālists elektronikas jomā, pats savā darbībā nevar apiet Ohmas likumu, atrisinot visas problēmas, kas saistītas ar elektronisko un elektrisko shēmu iestatīšanu, iestatīšanu, labošanu.

Patiesībā visiem ir vajadzīga izpratne par šo likumu. Jo ikvienam ikdienas dzīvē ir jātiek galā ar elektrību.

Un, lai arī vācu fiziķa Ohma likumus paredz vidusskolas kurss, praksē tas ne vienmēr tiek mācīts savlaicīgi. Tāpēc mēs savā materiālā apsvērsim šādu dzīves jautājumiem būtisku tēmu un izskatīsim formulas uzrakstīšanas iespējas.

Atsevišķa sadaļa un pilnīga elektriskā ķēde

Apsverot elektrisko ķēdi no Ohma likuma piemērošanas shēmai, jāņem vērā divas iespējamās aprēķina iespējas: vienai sekcijai un pilnvērtīgai shēmai.

Elektriskās ķēdes strāvas sekcijas aprēķins

Ķēdes daļai, kā likums, tiek uzskatīta par ķēdes daļu, izslēdzot EML avotu, kā papildu iekšējo pretestību.

Tāpēc šajā gadījumā aprēķina formula izskatās vienkārša:

I = U / R,

Kur attiecīgi:

• Es - strāvas stiprums;
• U - pielietotais spriegums;
• R - pretestība.

Formulas interpretācija ir vienkārša - strāva, kas plūst gar noteiktu ķēdes daļu, ir proporcionāla tai pielietotajam spriegumam, un pretestība ir apgriezti proporcionāla.

Tā sauktais grafiskais “margrietiņa”, caur kuru tiek parādīts viss formulējumu variantu kopums, pamatojoties uz Ohmas likumiem. Ērts rīks kabatas glabāšanai: sektors “P” - enerģijas formulas; sektors “U” - sprieguma formulas; sektors “I” - pašreizējās formulas; sektors “R” - pretestības formulas

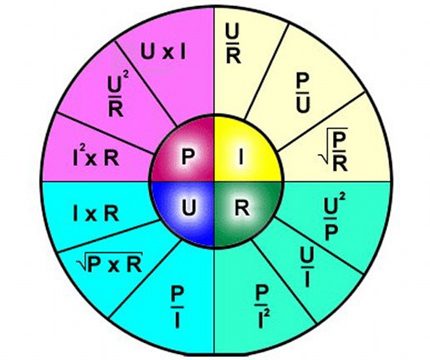
Tādējādi formula skaidri apraksta strāvas, kas plūst caur atsevišķu elektriskās ķēdes sadaļu, atkarību no noteiktām sprieguma un pretestības vērtībām.

Ērti ir izmantot formulu, piemēram, aprēķinot pretestības parametrus, kuri ir jāpielodē ķēdē, ja ir norādīts spriegums ar strāvu.

Ohmas likums un divas sekas, kas jābūt katram profesionālam elektriķim, elektrotehniķim, elektronikas inženierim un jebkuram, kas saistīts ar elektrisko ķēžu darbu. No kreisās uz labo: 1 - strāvas noteikšana; 2 - pretestības noteikšana; 3 - sprieguma noteikšana, kur I - strāvas stiprums, U - spriegums, R - pretestība

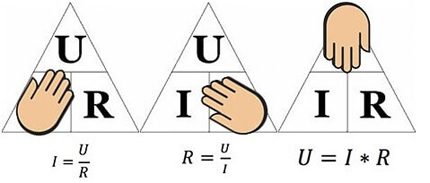
Iepriekš minētais skaitlis palīdzēs noteikt, piemēram, strāvu, kas plūst caur 10 omi pretestību, kurai tiek piemērots 12 voltu spriegums. Aizstājot vērtības, mēs atrodam - I = 12/10 = 1,2 ampēri.

Līdzīgi tiek risināti uzdevumi atrast pretestību (kad ir zināma strāva ar spriegumu) vai spriegumu (kad ir zināms spriegums ar strāvu).

Tādējādi vienmēr ir iespējams izvēlēties nepieciešamo darba spriegumu, nepieciešamo strāvas stiprumu un optimālo pretestības elementu.

Piedāvātajai formulai nav nepieciešams ņemt vērā sprieguma avota parametrus. Tomēr ķēde, kas satur, piemēram, akumulatoru, tiks aprēķināta, izmantojot citu formulu. Diagrammā: A - ampērmetra iekļaušana; V - voltmetra iekļaušana.

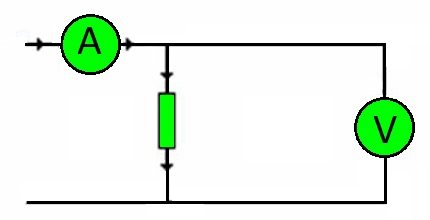
Starp citu, jebkuras ķēdes savienojošie vadi ir pretestība. Slodzes lielumu, kas viņiem jāuzņem, nosaka spriegums.

Attiecīgi, atkal izmantojot Ohma likumu, kļūst iespējams precīzi izvēlēties vajadzīgo vadītāja šķērsgriezumu atkarībā no serdes materiāla.

Vietnē ir sīki izstrādāti norādījumi kabeļa šķērsgriezums ar jaudu un strāvu.

Aprēķina iespēja pilnai ķēdei

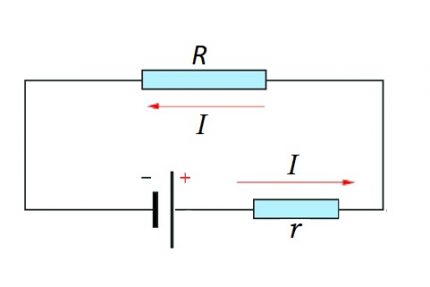
Pilnīga ķēde jau ir vietne (-es), kā arī EML avots. Tas ir, faktiski EML avota iekšējā pretestība tiek pievienota esošajai ķēdes sekcijas pretestībai.

Tāpēc loģiski ir dažas izmaiņas iepriekšminētajā formulā:

I = U / (R + r)

Protams, EML iekšējās pretestības vērtību Ohmas likumā par pilnīgu elektrisko ķēdi var uzskatīt par nenozīmīgu, lai gan daudzos aspektos šī pretestības vērtība ir atkarīga no EML avota struktūras.

Tomēr, aprēķinot sarežģītas elektroniskās shēmas, elektriskās shēmas ar daudziem vadītājiem, svarīgs faktors ir papildu pretestības klātbūtne.

Veicot aprēķinus pilnvērtīgā elektriskajā ķēdē, vienmēr ņem vērā EML avota pretestības vērtību. Šī vērtība tiek pievienota pašas elektriskās ķēdes pretestībai. Diagrammā: I - strāvas plūsma; R ir ārējais pretestības elements; r ir EML (enerģijas avota) pretestības koeficients

Gan ķēdes sadaļai, gan pilnīgai ķēdei jāņem vērā dabiskais moments - pastāvīgas vai mainīgas strāvas izmantošana.

Ja iepriekš minētie punkti, kas raksturīgi Ohmas likumiem, tika ņemti vērā no līdzstrāvas izmantošanas viedokļa, tad ar maiņstrāvu viss izskatās nedaudz savādāk.

Likuma izskatīšana mainīgam

Jēdziens "pretestība" maiņstrāvas caurlaidības apstākļiem būtu vairāk jāuzskata par "pretestības" jēdzienu. Šī ir aktīvās pretestības slodzes (Ra) un slodzes, ko veido reaktīvā pretestība (Rr), kombinācija.

Šādas parādības izraisa induktīvo elementu parametri un komutācijas likumi, ko piemēro mainīgai sprieguma vērtībai - sinusoidālai strāvas vērtībai.

Šķiet, ka šī ir maiņstrāvas elektriskās ķēdes ekvivalentā ķēde aprēķiniem, izmantojot formulējumus, kuru pamatā ir Ohma likuma principi: R - pretestības komponents; C ir kapacitīvā sastāvdaļa; L ir induktīvā sastāvdaļa; EML ir enerģijas avots; I-strāvas plūsma

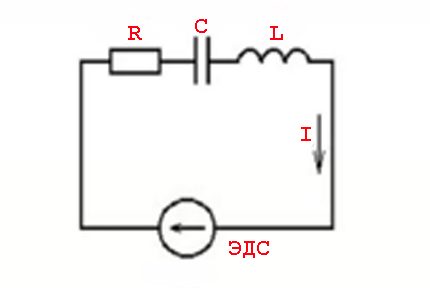
Citiem vārdiem sakot, rodas strāvas vērtību paaugstināšanās (atpalikšana) no sprieguma vērtībām, ko papildina aktīvās (pretestības) un reaktīvās (induktīvās vai kapacitīvās) spējas.

Šādu parādību aprēķināšanu veic, izmantojot formulu:

Z = U / I vai Z = R + J * (X_L - X_C)

kur: Z - pretestība; R - aktīvā slodze; X_L , X_C - induktīvā un kapacitīvā slodze; Dž - koeficients.

Elementu virkne un paralēlais savienojums

Elektriskās ķēdes (ķēdes sekcijas) elementiem raksturīgais moments ir virkne vai paralēls savienojums.

Attiecīgi katram savienojuma veidam tiek pievienots atšķirīgs strāvas plūsmas un sprieguma pievads. Šajā sakarā Ohmas likums tiek piemērots arī dažādos veidos, atkarībā no izvēles iekļaut elementus.

Rezistora ķēde

Saistībā ar seriālo savienojumu (ķēdes posmu ar diviem komponentiem) izmanto šādu formulu:

• I = i₁ = Es₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Šis formulējums skaidri parāda, ka neatkarīgi no virknē savienoto pretestīgo komponentu skaita shēmā plūstošā strāva nemainās.

Rezistīvo elementu savienojums ķēdes sekcijā virknē viens ar otru. Šai iespējai piemēro tās aprēķinu likumu. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U, U1, U2 - pielietotais spriegums

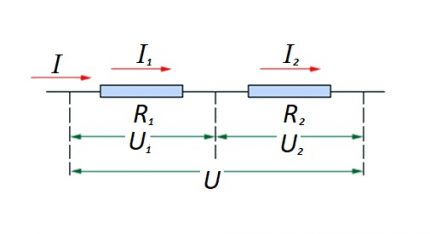
Ķēdes aktīvajām pretestīgajām sastāvdaļām piemērotā sprieguma lielums ir EMF avota kopējās vērtības summa.

Katras atsevišķas sastāvdaļas spriegums ir vienāds ar: Ux = I * Rx.

Kopējā pretestība jāuzskata par visu ķēdes pretestīgo komponentu nominālu summu.

Paralēli savienotu pretestības elementu ķēde

Gadījumā, ja pastāv pretestīgo komponentu savienojums, sekojoša formula tiek uzskatīta par taisnīgu attiecībā uz vācu fiziķa Ohma likumiem:

• I = i₁ + Es₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Nav izslēgtas iespējas jaukta tipa ķēžu sekciju sastādīšanai, ja tiek izmantots paralēlais un seriālais savienojums.

Resistīvo elementu savienojums ķēdē paralēli viens otram. Šai iespējai piemēro tās aprēķinu likumu. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U ir summētais spriegums; A, B - iebraukšanas / izbraukšanas punkti

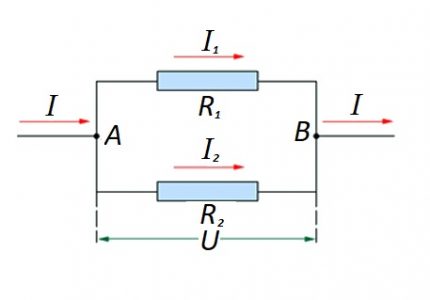
Šādām iespējām aprēķinu parasti veic, sākotnēji aprēķinot paralēlā savienojuma pretestības pakāpi. Tad rezultātam tiek pievienota virknē savienotā rezistora vērtība.

Integrālās un diferencētās tiesību formas

Visi iepriekš minētie aprēķinu punkti ir piemērojami apstākļiem, kad elektriskās ķēdēs tiek izmantoti “viendabīgas” struktūras vadītāji.

Tikmēr praksē bieži nākas saskarties ar ķēdes izbūvi, kurā vadītāju struktūra mainās dažādās jomās. Piemēram, tiek izmantoti lielāka šķērsgriezuma vai, gluži pretēji, mazāki vadi, kas izgatavoti, pamatojoties uz dažādiem materiāliem.

Lai ņemtu vērā šādas atšķirības, pastāv tā dēvētā "Ohma diferenciālā-integrālā likuma" variācija. Bezgalīgi mazam vadītājam strāvas blīvuma līmeni aprēķina atkarībā no stiprības un vadītspējas.

Saskaņā ar diferenciālo aprēķinu izmanto formulu: J = ό * E

Integrālajam aprēķinam attiecīgi: I * R = φ1 - φ2 + έ

Tomēr šie piemēri ir diezgan tuvāk augstākās matemātikas skolai, un praksē vienkāršs elektriķis faktiski netiek izmantots.

Secinājumi un noderīgs video par tēmu

Detalizēta Ohmas likuma analīze zemāk esošajā video palīdzēs beidzot nostiprināt zināšanas šajā virzienā.

Savdabīga video nodarbība kvalitatīvi pastiprina teorētisko rakstisko prezentāciju:

Elektriķa darbs vai elektronikas inženiera darbība ir nesaraujami saistīta ar brīžiem, kad jums patiešām darbībā ir jāievēro Georga Ohma likums. Šīs ir dažas izplatītas patiesības, kuras ikvienam profesionālam būtu jāzina.

Plašas zināšanas par šo jautājumu nav vajadzīgas - pietiek ar to, lai uzzinātu trīs galvenos formulējuma variantus, lai tos veiksmīgi piemērotu praksē.

Vai vēlaties papildināt iepriekš minēto materiālu ar vērtīgiem komentāriem vai izteikt savu viedokli? Lūdzu, rakstiet komentārus blokā zem raksta. Ja jums ir kādi jautājumi, droši jautājiet mūsu ekspertiem.