De wet van Ohm voor de volledige ketting en voor het gedeelte van de ketting: formules schrijven, beschrijving en uitleg

Een professionele elektricien, een gespecialiseerde elektronicus, kan de wet van Ohm niet omzeilen in zijn eigen activiteiten en lost alle problemen op die verband houden met het opzetten, afstemmen, repareren van elektronische en elektrische circuits.

Eigenlijk moet iedereen deze wet begrijpen. Omdat iedereen in het dagelijks leven met elektriciteit te maken heeft.

En hoewel de wet van de Duitse natuurkundige Ohm in een middelbare schoolopleiding wordt voorzien, wordt deze in de praktijk niet altijd tijdig bestudeerd. Daarom zullen we in ons materiaal zo'n onderwerp beschouwen dat relevant is voor het leven en we zullen de opties behandelen voor het schrijven van de formule.

Aparte sectie en compleet elektrisch circuit

Gezien het elektrische circuit vanuit het oogpunt van het toepassen van de wet van Ohm op het circuit, moeten twee mogelijke berekeningsopties worden opgemerkt: voor een enkele sectie en voor een volledig circuit.

Berekening van het huidige deel van het elektrische circuit

Het deel van het circuit wordt in de regel beschouwd als onderdeel van het circuit, met uitzondering van de bron van EMV, met extra interne weerstand.

Daarom ziet de berekeningsformule er in dit geval eenvoudig uit:

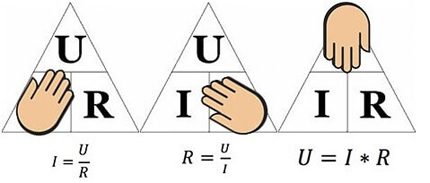
Ik = U / R,

Waar respectievelijk:

• Ik - huidige sterkte;
• U - aangelegde spanning;
• R - weerstand.

De interpretatie van de formule is eenvoudig: de stroom die langs een bepaald deel van het circuit stroomt, is evenredig met de spanning die erop wordt aangelegd en de weerstand is omgekeerd evenredig.

Het zogenaamde grafische 'madeliefje', waarmee de hele reeks variaties van formuleringen op basis van de wet van Ohm wordt gepresenteerd. Handig hulpmiddel voor zakopslag: sector “P” - krachtformules; sector "U" - spanningsformules; sector "I" - huidige formules; sector "R" - weerstandsformules

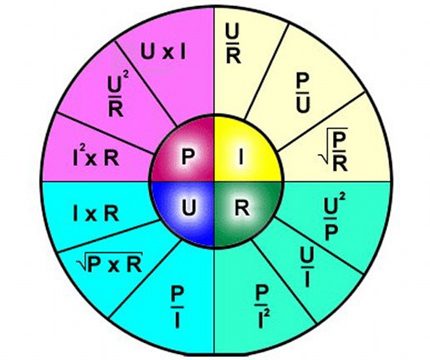
De formule beschrijft dus duidelijk de afhankelijkheid van de stroom die door een apart gedeelte van het elektrische circuit stroomt ten opzichte van bepaalde waarden van spanning en weerstand.

Het is handig om de formule te gebruiken, bijvoorbeeld om de weerstandsparameters te berekenen, die in het circuit moeten worden gesoldeerd als de spanning met stroom is gespecificeerd.

De wet van Ohm en twee gevolgen die elke professionele elektricien, elektrotechnisch ingenieur, elektrotechnisch ingenieur en iedereen die met het werk van elektrische circuits te maken heeft, moeten hebben. Van links naar rechts: 1 - stroomdetectie; 2 - bepaling van weerstand; 3 - spanningsbepaling, waarbij I - stroomsterkte, U - spanning, R - weerstand

De bovenstaande afbeelding helpt bijvoorbeeld bij het bepalen van de stroom die door een weerstand van 10 ohm stroomt, waarop een spanning van 12 volt wordt aangelegd. Als we de waarden vervangen, vinden we - I = 12/10 = 1,2 ampère.

Evenzo worden de taken van het vinden van weerstand (wanneer stroom met spanning bekend is) of spanning (wanneer spanning met stroom bekend is) opgelost.

Het is dus altijd mogelijk om de vereiste bedrijfsspanning, de vereiste stroomsterkte en het optimale weerstandselement te selecteren.

De formule die wordt voorgesteld om te worden gebruikt, vereist geen rekening houden met de parameters van de spanningsbron. Een circuit met bijvoorbeeld een batterij wordt echter berekend met een andere formule. In het diagram: A - opname van een ampèremeter; V - opname van de voltmeter.

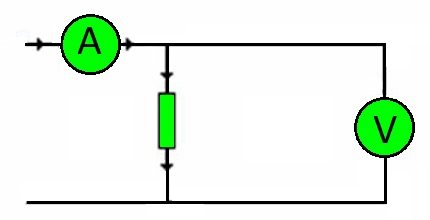
Trouwens, de verbindingsdraden van elk circuit zijn weerstand. De grootte van de belasting die ze moeten dragen, wordt bepaald door de spanning.

Dienovereenkomstig wordt het, opnieuw gebruikmakend van de wet van Ohm, mogelijk om nauwkeurig de noodzakelijke geleiderdoorsnede te selecteren, afhankelijk van het materiaal van de kern.

We hebben gedetailleerde instructies op de website kabeldoorsnede door stroom en stroom.

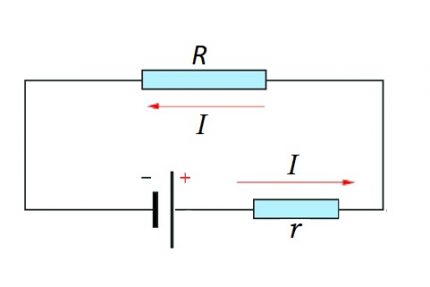
Berekeningsoptie voor volledige keten

Een complete keten is al de site (s), evenals de bron van EMF. Dat wil zeggen, in feite wordt de interne weerstand van de EMF-bron opgeteld bij de bestaande resistieve component van het circuitgedeelte.

Daarom is enige wijziging in de bovenstaande formule logisch:

Ik = U / (R + r)

Natuurlijk kan de waarde van de interne weerstand van de EMF in de wet van Ohm voor een volledig elektrisch circuit als verwaarloosbaar worden beschouwd, hoewel deze waarde van weerstand in veel opzichten afhangt van de structuur van de bron van EMF.

Bij het berekenen van complexe elektronische schakelingen, elektrische schakelingen met veel geleiders, is de aanwezigheid van extra weerstand echter een belangrijke factor.

Voor berekeningen in een volwaardig elektrisch circuit wordt altijd rekening gehouden met de weerstandswaarde van de EMF-bron. Deze waarde wordt opgeteld bij de weerstand van het elektrische circuit zelf. In het diagram: I - huidige stroom; R is het externe weerstandselement; r is de resistieve factor van de EMF (energiebron)

Voor zowel het circuitgedeelte als het volledige circuit moet rekening worden gehouden met het natuurlijke moment - het gebruik van een constante of variabele stroom.

Als de hierboven genoemde punten, kenmerkend voor de wet van Ohm, werden beschouwd vanuit het oogpunt van het gebruik van gelijkstroom, dan ziet alles er bij wisselstroom een ​​beetje anders uit.

Overweging van de wet naar een variabele

Het concept van "weerstand" tegen de doorgangsvoorwaarden van wisselstroom moet meer worden beschouwd als het concept van "impedantie". Dit is een combinatie van de actieve resistieve belasting (Ra) en de belasting gevormd door de reactieve weerstand (Rr).

Dergelijke verschijnselen worden veroorzaakt door de parameters van inductieve elementen en de wetten van schakelen zoals toegepast op een variabele spanningswaarde - een sinusvormige stroomwaarde.

Dit lijkt het equivalent circuit te zijn van een wisselstroom elektrisch circuit voor berekening met behulp van formuleringen gebaseerd op de principes van de wet van Ohm: R - resistieve component; C is de capacitieve component; L is de inductieve component; EMF is een energiebron; I-stroom

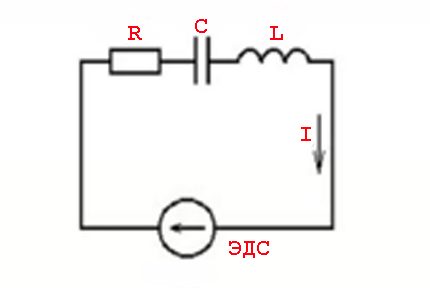
Met andere woorden, er is een effect van het voortschrijden van (achterblijvende) stroomwaarden uit spanningswaarden, wat gepaard gaat met het verschijnen van actieve (resistieve) en reactieve (inductieve of capacitieve) capaciteiten.

De berekening van dergelijke verschijnselen wordt uitgevoerd met de formule:

Z = U / I of Z = R + J * (X_L - X_C)

waar: Z - impedantie; R - actieve belasting; X_L , X_C - inductieve en capacitieve belasting; J - coëfficiënt.

Serie- en parallelschakeling van elementen

Voor elementen van een elektrisch circuit (circuitgedeelte) is een karakteristiek moment een serie- of parallelle verbinding.

Dienovereenkomstig gaat elk type verbinding gepaard met een andere aard van de stroom en stroomtoevoer. In dit opzicht is de wet van Ohm ook op verschillende manieren van toepassing, afhankelijk van de mogelijkheid om elementen op te nemen.

Weerstandscircuit

Met betrekking tot een seriële verbinding (een gedeelte van een circuit met twee componenten) wordt de volgende formule gebruikt:

• Ik = ik₁ = Ik₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Deze formulering laat duidelijk zien dat, ongeacht het aantal resistieve componenten die in serie zijn geschakeld, de stroom die in het circuit vloeit niet verandert.

Het in serie met elkaar verbinden van resistieve elementen in het circuitgedeelte. Voor deze optie is zijn eigen rekenwet van toepassing. In het diagram: I, I1, I2 - huidige stroom; R1, R2 - resistieve elementen; U, U1, U2 - aangelegde spanning

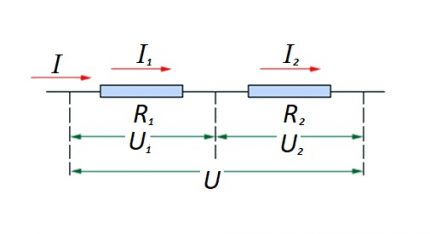
De grootte van de spanning die wordt toegepast op de actieve weerstandscomponenten van het circuit is de som van de totale waarde van de emf-bron.

De spanning op elk afzonderlijk onderdeel is gelijk aan: Ux = I * Rx.

De totale weerstand moet worden beschouwd als de som van de classificaties van alle resistieve componenten van het circuit.

Circuit van parallel geschakelde resistieve elementen

In het geval dat er een parallelle verbinding is tussen resistieve componenten, wordt de volgende formule als redelijk beschouwd met betrekking tot de wet van de Duitse natuurkundige Ohm:

• Ik = ik₁ + Ik₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Opties voor het samenstellen van circuitsecties van een "gemengd" type wanneer parallelle en seriële verbinding worden gebruikt, zijn niet uitgesloten.

De aansluiting van resistieve elementen in het circuit parallel aan elkaar. Voor deze optie is zijn eigen rekenwet van toepassing. In het diagram: I, I1, I2 - huidige stroom; R1, R2 - resistieve elementen; U is de opgetelde spanning; A, B - entry / exit-punten

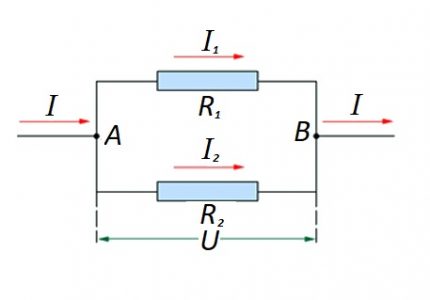
Voor dergelijke opties wordt de berekening meestal uitgevoerd door de eerste berekening van de resistieve beoordeling van de parallelle verbinding. Vervolgens wordt de waarde van de in serie geschakelde weerstand opgeteld bij het resultaat.

Integrale en differentiële rechtsvormen

Alle bovenstaande punten met de berekeningen zijn van toepassing op omstandigheden waarin geleiders met een "homogene" structuur worden gebruikt in de elektrische circuits.

Ondertussen heeft men in de praktijk vaak te maken met de constructie van een circuit waarbij de structuur van de geleiders op verschillende gebieden verandert. Er worden bijvoorbeeld draden gebruikt met een grotere doorsnede of juist kleinere, gemaakt op basis van verschillende materialen.

Om dergelijke verschillen te verklaren, is er een variatie op de zogenaamde "Ohm's differentiaalintegraalwet". Voor een oneindig kleine geleider wordt het huidige dichtheidsniveau berekend afhankelijk van de sterkte en geleidbaarheid.

Onder de differentiaalberekening wordt de formule genomen: J = ό * E

Voor integrale berekening respectievelijk de bewoording: Ik * R = φ1 - φ2 + έ

Deze voorbeelden liggen echter dichter bij de school voor hogere wiskunde en in de praktijk wordt een eenvoudige elektricien eigenlijk niet gebruikt.

Conclusies en nuttige video over het onderwerp

Een gedetailleerde analyse van de wet van Ohm in de onderstaande video zal helpen om eindelijk kennis in deze richting te consolideren.

Een bijzondere videoles versterkt kwalitatief de theoretische schriftelijke presentatie:

Het werk van een elektricien of de activiteit van een elektronische ingenieur is onlosmakelijk verbonden met momenten waarop je de wet van Georg Ohm in actie echt moet naleven. Dit zijn enkele veelvoorkomende waarheden die elke professional moet weten.

Uitgebreide kennis over dit onderwerp is niet vereist - het is voldoende om de drie belangrijkste variaties van de formulering te leren om met succes in de praktijk toe te passen.

Wilt u bovenstaand materiaal aanvullen met waardevolle opmerkingen of uw mening geven? Schrijf opmerkingen in het blok onder het artikel. Als u vragen heeft, stel ze dan gerust aan onze experts.