Ohms lov for hele kjeden og for seksjonen av kjeden: skrive formler, beskrivelse og forklaring

En profesjonell elektriker, en spesialisert elektronisk ingeniør, kan ikke komme seg rundt Ohms lov i sine egne aktiviteter, og løse eventuelle problemer forbundet med å sette opp, stille inn, reparere elektroniske og elektriske kretser.

Egentlig trenger alle en forståelse av denne loven. Fordi alle i hverdagen må takle strøm.

Og selv om loven til den tyske fysikeren Ohm er gitt av et ungdomsskolekurs, studeres den i praksis ikke alltid på en rettidig måte. Derfor vil vi i vårt materiale vurdere et slikt tema som er relevant for livet, og vi vil ta for oss alternativene for å skrive formelen.

Separat seksjon og komplett elektrisk krets

Tatt i betraktning den elektriske kretsen fra synspunktet om å anvende Ohms lov på kretsen, skal to mulige beregningsmuligheter bemerkes: for en enkelt seksjon og for en fullverdig krets.

Beregning av den gjeldende delen av den elektriske kretsen

Delen av kretsen regnes som regel som en del av kretsen, unntatt kilden til EMF, som har ytterligere intern motstand.

Derfor ser beregningsformelen i dette tilfellet enkel ut:

I = U / R,

Hvor:

• jeg - strømstyrke;
• U - påført spenning;
• R - motstand.

Tolkningen av formelen er enkel - strømmen som flyter langs en viss del av kretsen er proporsjonal med spenningen som påføres den, og motstanden er omvendt proporsjonal.

Den såkalte grafiske "tusenfryd", der hele settet med variasjoner av formuleringer basert på Ohms lov blir presentert. Praktisk verktøy for lommeoppbevaring: sektor “P” - kraftformler; sektor “U” - spenningsformler; sektor “I” - nåværende formler; sektor “R” - resistensformler

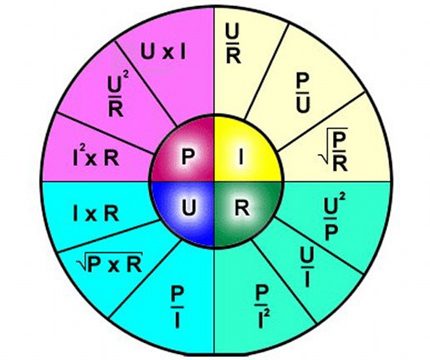
Formelen beskriver således tydelig avhengigheten av strømmen som strømmer gjennom en egen seksjon av den elektriske kretsen i forhold til visse spennings- og motstandsverdier.

Det er praktisk å bruke formelen, for eksempel å beregne motstandsparametrene, som må loddes inn i kretsen hvis spenningen med strøm er spesifisert.

Ohms lov og to konsekvenser som enhver profesjonell elektriker, elektroingeniør, elektronisk ingeniør og alle som er knyttet til arbeidet med elektriske kretser, må ha. Fra venstre mot høyre: 1 - strømdeteksjon; 2 - bestemmelse av motstand; 3 - spenningsbestemmelse, hvor I - strømstyrke, U - spenning, R - motstand

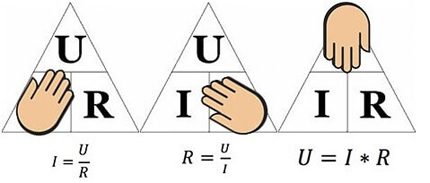
Figuren ovenfor vil bidra til å bestemme for eksempel strømmen som strømmer gjennom en 10 ohm-motstand, som en spenning på 12 volt tilføres. Ved å erstatte verdiene finner vi - I = 12/10 = 1,2 ampere.

Tilsvarende løses oppgavene med å finne motstand (når strøm med spenning er kjent) eller spenning (når spenning med strøm er kjent).

Dermed er det alltid mulig å velge ønsket driftsspenning, den nødvendige strømstyrken og det optimale motstandselementet.

Formelen som foreslås brukt, krever ikke å ta hensyn til parametrene til spenningskilden. Imidlertid vil en krets som inneholder for eksempel et batteri beregnes ved å bruke en annen formel. I diagrammet: A - inkludering av et ammeter; V - inkludering av voltmeteret.

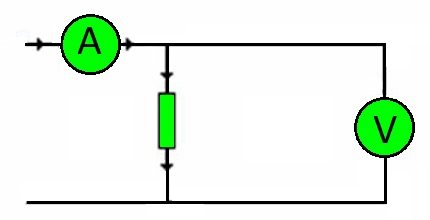
Forresten, tilkoblingstrådene til enhver krets er motstand. Størrelsen på belastningen de må bære, bestemmes av spenningen.

Følgelig, igjen ved å bruke Ohms lov, blir det mulig å nøyaktig velge nødvendig ledertverrsnitt, avhengig av kjernen.

Vi har detaljerte instruksjoner på nettstedet kabeltverrsnitt etter strøm og strøm.

Beregningsalternativ for full kjede

En komplett kjede er allerede nettstedet (r), samt kilden til EMF. Det vil si at den interne motstanden til EMF-kilden blir lagt til den eksisterende motstandsdyktige komponenten i kretsseksjonen.

Derfor er noen endringer i formelen ovenfor logiske:

I = U / (R + r)

Selvfølgelig kan verdien av den interne motstanden til EMF i Ohms lov for en komplett elektrisk krets betraktes som ubetydelig, selv om denne resistensverdien i mange henseender avhenger av strukturen til EMF-kilden.

Når man beregner komplekse elektroniske kretsløp, elektriske kretser med mange ledere, er imidlertid tilstedeværelsen av ekstra motstand en viktig faktor.

Ved beregninger i en fullverdig elektrisk krets tas alltid resistivverdien til EMF-kilden med i betraktningen. Denne verdien tillegges motstanden til selve den elektriske kretsen. I diagrammet: I - strømflyt; R er det resistive elementet eksternt; r er den resistive faktoren til EMF (energikilde)

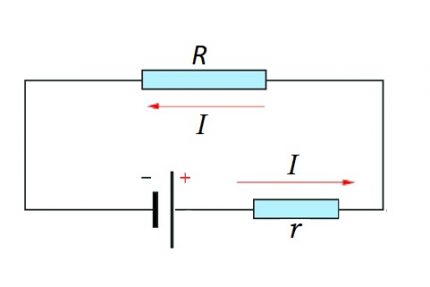
For både kretsseksjonen og hele kretsen, bør det naturlige øyeblikket tas i betraktning - bruk av konstant eller variabel strøm.

Hvis punktene som er nevnt ovenfor, karakteristiske for Ohms lov, ble vurdert fra synspunktet om å bruke likestrøm, i samsvar med vekselstrøm ser alt litt annerledes ut.

Hensynet til loven til en variabel

Begrepet "motstand" mot betingelsene for passering av vekselstrøm bør betraktes mer som begrepet "impedans". Dette er en kombinasjon av den aktive resistive belastningen (Ra) og belastningen dannet av den reaktive motstanden (Rr).

Slike fenomener er forårsaket av parametrene til induktive elementer og lovene for å bytte som anvendt på en variabel spenningsverdi - en sinusformet strømverdi.

Dette ser ut til å være den ekvivalente kretsen til en vekselstrømskrets for beregning ved bruk av formuleringer basert på prinsippene i Ohms lov: R - resistiv komponent; C er den kapasitive komponenten; L er den induktive komponenten; EMF er en energikilde; Jeg-strøm

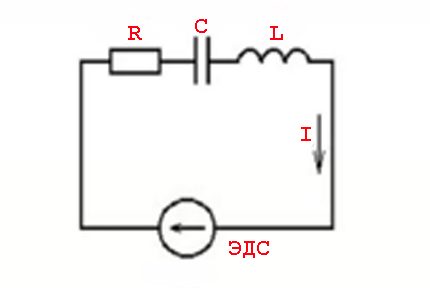
Med andre ord er det en effekt av å flytte (hale) strømverdier fra spenningsverdier, som er ledsaget av utseendet til aktive (resistive) og reaktive (induktive eller kapasitive) kapasiteter.

Beregningen av slike fenomener blir utført ved å bruke formelen:

Z = U / I eller Z = R + J * (X_L - X_C)

der: Z - impedans; R - aktiv belastning; X_L , X_C - induktiv og kapasitiv belastning; J - koeffisient.

Serier og parallell tilkobling av elementer

For elementer i en elektrisk krets (kretsdel) er et karakteristisk moment en serie eller parallell forbindelse.

Følgelig er hver type forbindelse forbundet med en annen karakter av strømnings- og spenningsforsyningen. I denne forbindelse gjelder Ohms lov også på forskjellige måter, avhengig av muligheten for å inkludere elementer.

Motstandskrets

I forhold til en seriell forbindelse (en del av en krets med to komponenter), brukes følgende formel:

• Jeg = jeg₁ = Jeg₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Denne formuleringen demonstrerer tydelig at uansett antall motstandsdyktige komponenter koblet i serie, endrer ikke strømmen i kretsen seg.

Forbindelsen av resistive elementer i kretsseksjonen i serie med hverandre. For dette alternativet gjelder egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U, U1, U2 - påført spenning

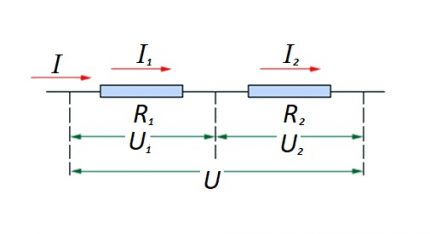
Størrelsen på spenningen som påføres de aktive resistive komponentene i kretsen er summen av den totale verdien av emk-kilden.

Spenningen på hver enkelt komponent er lik: Ux = I * Rx.

Den totale motstanden bør betraktes som summen av klassifiseringen av alle de resistive komponentene i kretsen.

Krets av parallelle tilkoblede resistive elementer

I tilfelle der det er en parallell forbindelse av resistive komponenter, anses følgende formel å være rettferdig med hensyn til loven til den tyske fysikeren Ohm:

• Jeg = jeg₁ + Jeg₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Alternativer for å sammenstille kretsseksjoner av en "blandet" type når parallell og seriell tilkobling brukes er ikke utelukket.

Koblingen av resistive elementer i kretsen parallelt med hverandre. For dette alternativet gjelder egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U er den summerte spenningen; A, B - inngangs- / utgangspunkter

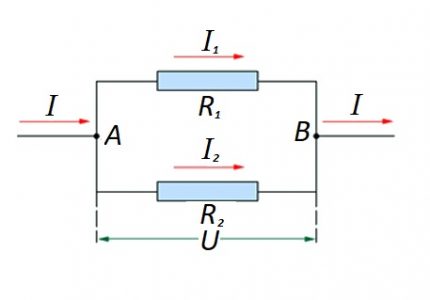
For slike alternativer utføres beregningen vanligvis ved den første beregningen av den resistive graden av parallellforbindelsen. Deretter blir verdien av motstanden som er koblet i serie lagt til resultatet.

Integrerte og differensielle rettsformer

Alle ovennevnte punkter med beregningene gjelder for forhold når ledere med en "homogen" struktur brukes i de elektriske kretsene.

I mellomtiden må man i praksis ofte forholde seg til konstruksjonen av en krets der strukturen til lederne endres på forskjellige områder. For eksempel brukes ledninger med større tverrsnitt eller tvert imot mindre, laget på basis av forskjellige materialer.

For å redegjøre for slike forskjeller, er det en variasjon av den såkalte "Ohms differensialintegrale lov". For en uendelig liten leder beregnes strømtetthetsnivået avhengig av styrke og ledningsevne.

Under differensialberegningen er formelen tatt: J = ό * E

For integrert beregning, henholdsvis, formuleringen: I * R = φ1 - φ2 + έ

Imidlertid er disse eksemplene ganske nærmere skolen for høyere matematikk, og i faktisk praksis brukes faktisk ikke en enkel elektriker.

Konklusjoner og nyttig video om emnet

En detaljert analyse av Ohms lov i videoen nedenfor vil hjelpe til med å endelig befeste kunnskap i denne retningen.

En særegen videotime forsterker kvalitativt den teoretiske skriftlige presentasjonen:

Arbeidet til en elektriker eller aktiviteten til en elektronisk ingeniør er uløselig knyttet til øyeblikk når du virkelig må følge Georg Ohms lov i aksjon. Dette er noen vanlige sannheter som enhver profesjonell bør kjenne til.

Omfattende kunnskap om dette spørsmålet er ikke nødvendig - det er nok å lære de tre viktigste variantene av ordlyden for å kunne bruke i praksis.

Vil du supplere materialet ovenfor med verdifulle kommentarer eller uttrykke din mening? Skriv kommentarer i blokken under artikkelen. Hvis du har spørsmål, kan du gjerne spørre våre eksperter.