กฎของโอห์มสำหรับห่วงโซ่ที่สมบูรณ์และในส่วนของโซ่: สูตรการเขียนคำอธิบายและคำอธิบาย

ช่างไฟฟ้ามืออาชีพวิศวกรอิเล็กทรอนิกส์ผู้เชี่ยวชาญไม่สามารถทำตามกฎหมายของโอห์มในกิจกรรมของตัวเองแก้ปัญหาใด ๆ ที่เกี่ยวข้องกับการติดตั้งปรับซ่อมวงจรอิเล็กทรอนิกส์และวงจรไฟฟ้า

จริงๆแล้วทุกคนต้องการความเข้าใจในกฎหมายนี้ เพราะทุกคนในชีวิตประจำวันต้องรับมือกับกระแสไฟฟ้า

และถึงแม้ว่ากฎของนักฟิสิกส์ชาวเยอรมันโอห์มนั้นจัดทำขึ้นโดยหลักสูตรระดับมัธยมศึกษา แต่ในทางปฏิบัติมันไม่ได้มีการศึกษาในเวลาที่เหมาะสมเสมอไป ดังนั้นเราจะพิจารณาเนื้อหาของเราในหัวข้อที่เกี่ยวข้องกับชีวิตและเราจะจัดการกับตัวเลือกสำหรับการเขียนสูตร

แยกส่วนและวงจรไฟฟ้าที่สมบูรณ์

เมื่อพิจารณาวงจรไฟฟ้าจากมุมมองของการใช้กฎของโอห์มกับวงจรควรคำนึงถึงตัวเลือกการคำนวณที่เป็นไปได้สองแบบ: สำหรับส่วนเดียวและสำหรับวงจรเต็มรูปแบบ

การคำนวณส่วนปัจจุบันของวงจรไฟฟ้า

ส่วนหนึ่งของวงจรนั้นเป็นส่วนหนึ่งของวงจรโดยไม่รวมถึงแหล่งกำเนิดของ EMF เนื่องจากมีความต้านทานภายในเพิ่มเติม

ดังนั้นสูตรการคำนวณในกรณีนี้จึงดูเรียบง่าย:

I = U / R,

ที่ไหนตามลำดับ:

• ผม - ความแข็งแรงในปัจจุบัน
• U - แรงดันไฟฟ้าที่ใช้
• R - ความต้านทาน

การตีความของสูตรนั้นง่ายมาก - กระแสที่ไหลไปตามส่วนหนึ่งของวงจรนั้นเป็นสัดส่วนกับแรงดันไฟฟ้าที่ใช้กับมันและความต้านทานนั้นแปรผันตามสัดส่วน

กราฟิกที่เรียกว่า "เดซี่" ซึ่งมีการเปลี่ยนแปลงสูตรทั้งหมดตามกฎหมายของโอห์ม เครื่องมือที่สะดวกสำหรับการจัดเก็บกระเป๋า: เซกเตอร์“ P” - สูตรพลังงาน เซกเตอร์“ U” - สูตรแรงดันไฟฟ้า ภาค“ ฉัน” - สูตรปัจจุบัน ภาค“ R” - สูตรต้านทาน

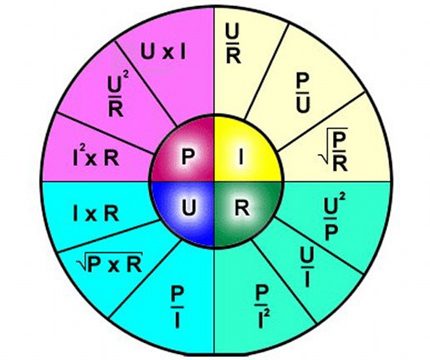
ดังนั้นสูตรอธิบายอย่างชัดเจนถึงการพึ่งพาของกระแสที่ไหลผ่านส่วนที่แยกต่างหากของวงจรไฟฟ้าที่สัมพันธ์กับค่าบางอย่างของแรงดันไฟฟ้าและความต้านทาน

มันสะดวกที่จะใช้สูตรเช่นการคำนวณค่าความต้านทานซึ่งจะต้องบัดกรีเข้าสู่วงจรหากระบุแรงดันไฟฟ้าที่มีกระแส

กฎของโอห์มและสองสิ่งที่ตามมาคือช่างไฟฟ้ามืออาชีพวิศวกรไฟฟ้าวิศวกรอิเล็กทรอนิกส์และทุกคนที่เกี่ยวข้องกับการทำงานของวงจรไฟฟ้าจะต้องมี จากซ้ายไปขวา: 1 - การตรวจจับกระแส 2 - การกำหนดความต้านทาน การกำหนดแรงดันไฟฟ้า 3 ระดับที่แรงกระแส I, แรงดัน U, ความต้านทาน R

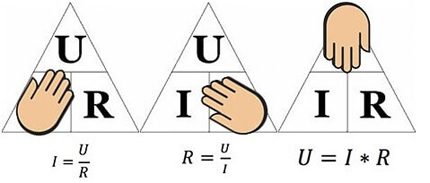
รูปด้านบนจะช่วยพิจารณาตัวอย่างเช่นกระแสที่ไหลผ่านความต้านทาน 10 โอห์มซึ่งจะใช้แรงดันไฟฟ้า 12 โวลต์ แทนที่ค่าเราพบ - I = 12/10 = 1.2 แอมแปร์

ในทำนองเดียวกันงานของการค้นหาความต้านทาน (เมื่อทราบกระแสกับแรงดันไฟฟ้า) หรือแรงดัน (เมื่อทราบแรงดันกับกระแส) จะถูกแก้ไข

ดังนั้นจึงเป็นไปได้เสมอที่จะเลือกแรงดันไฟฟ้าที่ต้องการกระแสไฟฟ้าที่ต้องการและองค์ประกอบความต้านทานที่เหมาะสม

สูตรที่เสนอให้ใช้ไม่จำเป็นต้องคำนึงถึงพารามิเตอร์ของแหล่งจ่ายแรงดัน อย่างไรก็ตามวงจรที่มีตัวอย่างเช่นแบตเตอรี่จะถูกคำนวณโดยใช้สูตรอื่น ในแผนภาพ: A - รวมแอมป์มิเตอร์; V - รวมของโวลต์มิเตอร์

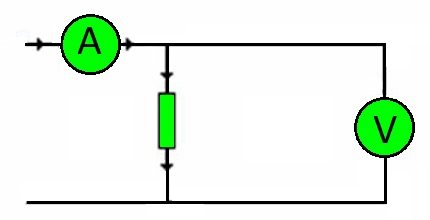
โดยวิธีการเชื่อมต่อสายไฟของวงจรใด ๆ ที่มีความต้านทาน ขนาดของภาระที่ต้องแบกขึ้นอยู่กับแรงดันไฟฟ้า

ดังนั้นโดยใช้กฎของโอห์มอีกครั้งมันเป็นไปได้ที่จะเลือกตัวนำที่จำเป็นข้ามส่วนได้อย่างถูกต้องขึ้นอยู่กับวัสดุของแกนกลาง

เรามีคำแนะนำโดยละเอียดเกี่ยวกับเว็บไซต์ สายเคเบิลข้ามส่วน โดยพลังงานและปัจจุบัน

ตัวเลือกการคำนวณสำหรับเต็มโซ่

เครือข่ายที่สมบูรณ์นั้นเป็นไซต์อยู่แล้วรวมถึงแหล่งที่มาของ EMF นั่นคือในความเป็นจริงความต้านทานภายในของแหล่ง EMF จะถูกเพิ่มเข้าไปในองค์ประกอบความต้านทานที่มีอยู่ของส่วนวงจร

ดังนั้นการเปลี่ยนแปลงบางอย่างของสูตรด้านบนจึงมีเหตุผล:

I = U / (R + r)

แน่นอนว่าค่าความต้านทานภายในของ EMF ในกฎของโอห์มสำหรับวงจรไฟฟ้าที่สมบูรณ์นั้นอาจพิจารณาเล็กน้อยแม้ว่าในหลาย ๆ แง่มุมของค่าความต้านทานนี้ขึ้นอยู่กับโครงสร้างของแหล่งที่มาของ EMF

อย่างไรก็ตามเมื่อทำการคำนวณวงจรอิเล็กทรอนิกส์ที่ซับซ้อนวงจรไฟฟ้าที่มีตัวนำหลายตัวการมีความต้านทานเพิ่มเติมเป็นปัจจัยสำคัญ

สำหรับการคำนวณในวงจรไฟฟ้าที่มีประจุเต็มจะพิจารณาค่าความต้านทานของแหล่งกำเนิด EMF เสมอ ค่านี้จะเพิ่มความต้านทานของวงจรไฟฟ้าเอง ในแผนภาพ: I - กระแสไหล R คือองค์ประกอบต้านทานภายนอก r คือปัจจัยต้านทานของ EMF (แหล่งพลังงาน)

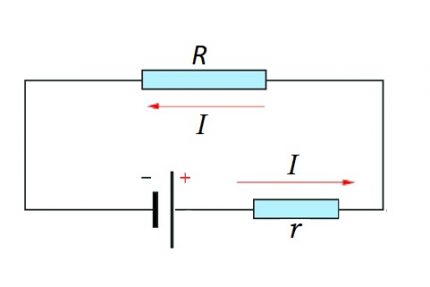
สำหรับทั้งส่วนของวงจรและวงจรสมบูรณ์ควรคำนึงถึงช่วงเวลาที่เป็นธรรมชาติซึ่ง ได้แก่ การใช้กระแสคงที่หรือตัวแปร

หากคะแนนที่ระบุไว้ข้างต้นลักษณะของกฎของโอห์มได้รับการพิจารณาจากมุมมองของการใช้กระแสตรงดังนั้นด้วยการสลับกระแสทุกอย่างดูแตกต่างกันเล็กน้อย

การพิจารณาของกฎหมายต่อตัวแปร

แนวคิดของ "การต่อต้าน" กับเงื่อนไขของทางเดินของกระแสสลับควรพิจารณาเพิ่มเติมว่าเป็นแนวคิดของ "อิมพีแดนซ์" นี่คือการรวมกันของโหลดตัวต้านทานที่ใช้งาน (Ra) และโหลดที่เกิดขึ้นจากตัวต้านทานปฏิกิริยา (Rr)

ปรากฏการณ์ดังกล่าวเกิดจากพารามิเตอร์ขององค์ประกอบที่เหนี่ยวนำและกฎของการสลับที่ใช้กับค่าแรงดันไฟฟ้าตัวแปร - มูลค่าปัจจุบันของไซน์

นี่น่าจะเป็นวงจรสมมูลของวงจรไฟฟ้ากระแสสลับสำหรับการคำนวณโดยใช้สูตรตามหลักการของกฎของโอห์ม: ส่วนประกอบต้านทานทาน C เป็นองค์ประกอบ capacitive L เป็นองค์ประกอบอุปนัย EMF เป็นแหล่งพลังงาน กระแส I- ปัจจุบัน

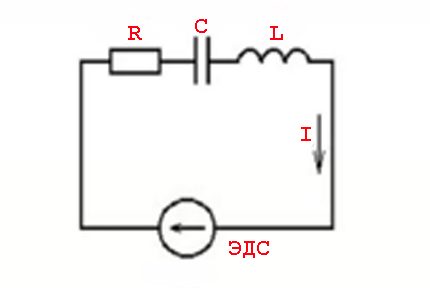
กล่าวอีกนัยหนึ่งมีผลกระทบของความก้าวหน้า (ปกคลุมด้วยวัตถุฉนวน) ค่าปัจจุบันจากค่าแรงดันไฟฟ้าซึ่งมาพร้อมกับลักษณะของการใช้งาน (ตัวต้านทาน) และความจุปฏิกิริยา (อุปนัยหรือ capacitive)

การคำนวณปรากฏการณ์ดังกล่าวดำเนินการโดยใช้สูตร:

Z = U / I หรือ Z = R + J * (X_L - X_C)

ที่อยู่: Z - ความต้านทาน R - โหลดที่ใช้งาน X_L , X_C - โหลดอุปนัยและ capacitive; J - สัมประสิทธิ์

การเชื่อมต่ออนุกรมและองค์ประกอบแบบขนาน

สำหรับองค์ประกอบของวงจรไฟฟ้า (ส่วนวงจร) ช่วงเวลาพิเศษคือการเชื่อมต่อแบบอนุกรมหรือแบบขนาน

ดังนั้นการเชื่อมต่อแต่ละประเภทจะมาพร้อมกับลักษณะที่แตกต่างกันของการไหลของกระแสและแรงดันไฟฟ้า ในเรื่องนี้กฎของโอห์มก็มีผลบังคับใช้ในหลายวิธีขึ้นอยู่กับตัวเลือกในการรวมองค์ประกอบต่างๆ

วงจรตัวต้านทาน

ในส่วนที่เกี่ยวกับการเชื่อมต่อแบบอนุกรม (ส่วนหนึ่งของวงจรที่มีสององค์ประกอบ) จะใช้สูตรต่อไปนี้:

• ฉัน = ฉัน₁ = ฉัน₂ ;
• U = U₁ + คุณ₂ ;
• R = R₁ + R₂

สูตรนี้แสดงให้เห็นอย่างชัดเจนว่าไม่ว่าจะมีส่วนประกอบตัวต้านทานใด ๆ ที่เชื่อมต่อแบบอนุกรมกระแสไฟฟ้าในวงจรจะไม่เปลี่ยนแปลง

การเชื่อมต่อขององค์ประกอบต้านทานในส่วนวงจรในซีรีส์กับอีกคนหนึ่ง สำหรับตัวเลือกนี้จะใช้กฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - การไหลของกระแส R1, R2 - องค์ประกอบต้านทาน U, U1, U2 - แรงดันไฟฟ้าที่ใช้

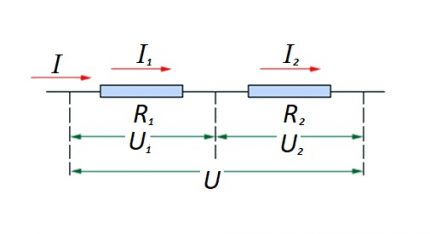
ขนาดของแรงดันไฟฟ้าที่ใช้กับส่วนประกอบตัวต้านทานแบบแอกทีฟของวงจรคือผลรวมของมูลค่ารวมของแหล่งกำเนิดคลื่น

แรงดันไฟฟ้าในแต่ละองค์ประกอบเท่ากับ: Ux = I * Rx.

ความต้านทานรวมควรพิจารณาเป็นผลรวมของคะแนนของส่วนประกอบต้านทานทั้งหมดของวงจร

วงจรขององค์ประกอบตัวต้านทานที่เชื่อมต่อแบบขนาน

ในกรณีที่มีการเชื่อมต่อแบบขนานของส่วนประกอบตัวต้านทานสูตรต่อไปนี้จะถือว่ายุติธรรมตามกฎหมายของนักฟิสิกส์ชาวเยอรมันโอห์ม:

• ฉัน = ฉัน₁ + ฉัน₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

ตัวเลือกสำหรับการรวบรวมส่วนวงจรของชนิด“ ผสม” เมื่อใช้การเชื่อมต่อแบบขนานและอนุกรมจะไม่ถูกตัดออก

การเชื่อมต่อขององค์ประกอบต้านทานในวงจรขนานกับอีกคนหนึ่ง สำหรับตัวเลือกนี้จะใช้กฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - การไหลของกระแส R1, R2 - องค์ประกอบต้านทาน U คือแรงดันไฟฟ้ารวม A, B - จุดเข้า / ออก

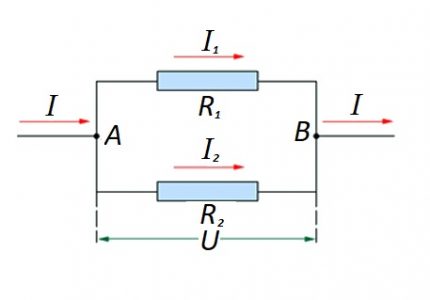
สำหรับตัวเลือกดังกล่าวการคำนวณมักจะดำเนินการโดยการคำนวณเริ่มต้นของการจัดอันดับความต้านทานของการเชื่อมต่อแบบขนาน จากนั้นค่าของตัวต้านทานที่เชื่อมต่อเป็นอนุกรมจะถูกเพิ่มเข้าไปในผลลัพธ์

รูปแบบของกฎหมายที่สมบูรณ์และแตกต่างกัน

จุดทั้งหมดข้างต้นที่มีการคำนวณจะใช้กับเงื่อนไขเมื่อตัวนำของโครงสร้าง“ เอกพันธ์” ถูกใช้ในวงจรไฟฟ้า

ในทางปฏิบัติเรามักจะต้องจัดการกับการสร้างวงจรที่โครงสร้างของตัวนำมีการเปลี่ยนแปลงในพื้นที่ต่าง ๆ ตัวอย่างเช่นใช้ลวดที่มีขนาดใหญ่กว่าหรือในทางตรงกันข้ามจะใช้ลวดที่มีขนาดเล็กกว่าซึ่งทำจากวัสดุที่แตกต่างกัน

เพื่ออธิบายความแตกต่างดังกล่าวมีการเปลี่ยนแปลงของสิ่งที่เรียกว่า สำหรับตัวนำขนาดเล็กแบบไม่ จำกัด ระดับความหนาแน่นกระแสจะถูกคำนวณขึ้นอยู่กับความแข็งแรงและการนำไฟฟ้า

ภายใต้การคำนวณที่แตกต่างสูตรจะถูกนำมาใช้: J = ό * E

สำหรับการคำนวณแบบรวมตามลำดับข้อความ: I * R = φ1 - φ2 + έ

อย่างไรก็ตามตัวอย่างเหล่านี้ค่อนข้างใกล้กับโรงเรียนคณิตศาสตร์ขั้นสูงและในทางปฏิบัติแล้วช่างไฟฟ้าธรรมดาไม่ได้ใช้จริง

ข้อสรุปและวิดีโอที่มีประโยชน์ในหัวข้อ

การวิเคราะห์โดยละเอียดของกฎของโอห์มในวิดีโอด้านล่างจะช่วยในการรวบรวมความรู้ในทิศทางนี้ในที่สุด

บทเรียนวิดีโอที่แปลกประหลาดในเชิงคุณภาพตอกย้ำการนำเสนอเชิงทฤษฎี:

การทำงานของช่างไฟฟ้าหรือกิจกรรมของวิศวกรอิเล็กทรอนิกส์นั้นเชื่อมโยงกับช่วงเวลาที่คุณต้องปฏิบัติตามกฎหมายของ Georg Ohm อย่างจริงจัง นี่คือความจริงทั่วไปบางประการที่นักวิชาชีพทุกคนควรรู้

ไม่จำเป็นต้องมีความรู้อย่างกว้างขวางเกี่ยวกับปัญหานี้ - มันเพียงพอที่จะเรียนรู้การใช้ถ้อยคำหลัก ๆ สามแบบเพื่อนำไปใช้ในทางปฏิบัติได้สำเร็จ

คุณต้องการที่จะเสริมเนื้อหาข้างต้นด้วยความเห็นที่มีคุณค่าหรือแสดงความคิดเห็นของคุณ? กรุณาเขียนความคิดเห็นในบล็อกภายใต้บทความ หากคุณมีคำถามใด ๆ โปรดถามผู้เชี่ยวชาญของเรา