Bütün zincir ve zincir bölümü için Ohm yasası: formül yazma, açıklama ve açıklama
Profesyonel bir elektrikçi, uzman bir elektronik mühendisi, Ohm yasasını kendi faaliyetlerinde ele alamaz, elektronik ve elektrik devrelerinin kurulması, ayarlanması, onarılması ile ilgili herhangi bir sorunu çözemez.
Aslında, herkesin bu yasayı anlamasına ihtiyaç var. Çünkü günlük yaşamdaki herkes elektrikle uğraşmak zorunda.
Ve Alman fizikçi Ohm yasası bir ortaokul kursu tarafından sağlansa da, pratikte her zaman zamanında incelenmemektedir. Bu nedenle, materyalimizde yaşamla ilgili bir konuyu ele alacağız ve formülü yazma seçenekleri ile ilgileneceğiz.
Makalenin içeriği:
Ayrı bölüm ve komple elektrik devresi
Elektrik devresini Ohm yasasının devreye uygulanması açısından dikkate alındığında, iki olası hesaplama seçeneğine dikkat edilmelidir: tek bir bölüm ve tam teşekküllü bir devre için.
Elektrik devresinin akım bölümünün hesaplanması
Devrenin bir kısmı, kural olarak, EMF kaynağı hariç, ek iç dirence sahip olarak devrenin bir parçası olarak kabul edilir.
Bu nedenle, bu durumda hesaplama formülü basit görünüyor:
I = U / R,
Sırasıyla nerede:
- ben - akım gücü;
- U - uygulanan voltaj;
- R, - direnç.
Formülün yorumlanması basittir - devrenin belirli bir kısmı boyunca akan akım, ona uygulanan voltajla orantılıdır ve direnç ters orantılıdır.
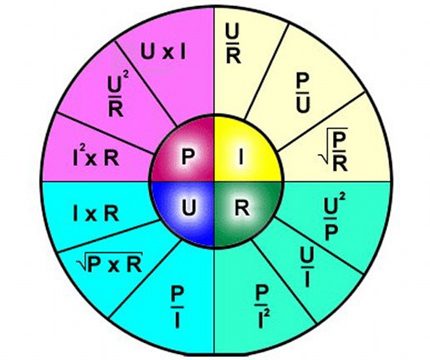
Böylece formül, elektrik devresinin ayrı bir bölümünden akan akımın belirli voltaj ve direnç değerlerine göre bağımlılığını açıkça tanımlar.
Formülü kullanmak, örneğin, akım ile voltaj belirtilirse, devreye lehimlenmesi gereken direnç parametrelerini hesaplamak uygundur.
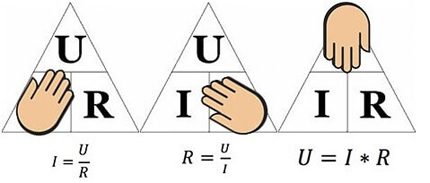
Yukarıdaki şekil, örneğin, 12 voltluk bir voltajın uygulandığı 10 ohm'luk bir dirençten akan akımın belirlenmesine yardımcı olacaktır. Değerleri değiştirerek - I = 12/10 = 1.2 amper buluyoruz.
Benzer şekilde, direnç (voltajlı akım biliniyorsa) veya voltaj (akımla voltaj biliniyorsa) bulma görevleri de çözülür.
Bu nedenle, gerekli çalışma voltajını, gerekli amperi ve optimum direnç elemanını seçmek her zaman mümkündür.
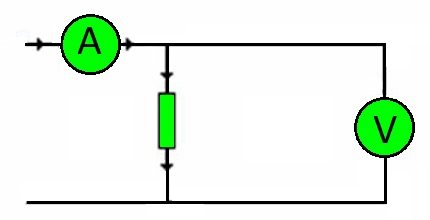
Bu arada, herhangi bir devrenin bağlantı telleri dirençtir. Taşımaları gereken yükün büyüklüğü voltaj tarafından belirlenir.
Buna göre, yine Ohm yasasını kullanarak, çekirdeğin malzemesine bağlı olarak gerekli iletken kesitini doğru bir şekilde seçmek mümkün hale gelir.
Web sitesinde ayrıntılı talimatlarımız var kablo kesiti güç ve akım ile.
Tam Zincir için Hesaplama Seçeneği
Tam bir zincir hali hazırda EMF'nin yanı sıra saha (lar) dadır. Yani, EMF kaynağının iç direnci, devre bölümünün mevcut rezistif bileşenine eklenir.
Bu nedenle, yukarıdaki formülde bazı değişiklikler mantıklıdır:
I = U / (R + r)
Tabii ki, tam bir elektrik devresi için Ohm yasasında EMF'nin iç direncinin değeri ihmal edilebilir olarak değerlendirilebilir, ancak birçok bakımdan bu direnç değeri EMF kaynağının yapısına bağlıdır.
Bununla birlikte, karmaşık elektronik devreler, birçok iletkenli elektrik devreleri hesaplanırken, ek direnç varlığı önemli bir faktördür.
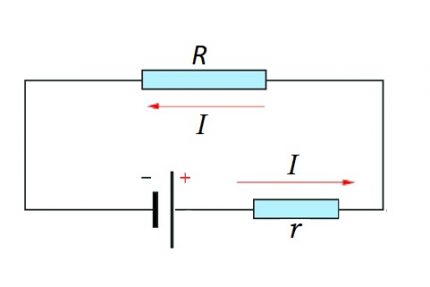
Hem devre bölümü hem de tüm devre için doğal moment dikkate alınmalıdır - sabit veya değişken bir akım kullanımı.
Yukarıda belirtilen noktalar, Ohm yasasının karakteristiği, doğru akım kullanma açısından düşünüldüğünde, alternatif akıma göre her şey biraz farklı görünüyor.
Bir değişkene göre kanunun dikkate alınması
Alternatif akım geçiş koşullarına "direnç" kavramı daha çok "empedans" kavramı olarak düşünülmelidir. Bu, aktif direnç yükünün (Ra) ve reaktif direnç (Rr) tarafından oluşturulan yükün bir kombinasyonudur.
Bu fenomenler, endüktif elemanların parametreleri ve değişken bir voltaj değerine - sinüzoidal akım değerine uygulanan anahtarlama yasalarından kaynaklanır.
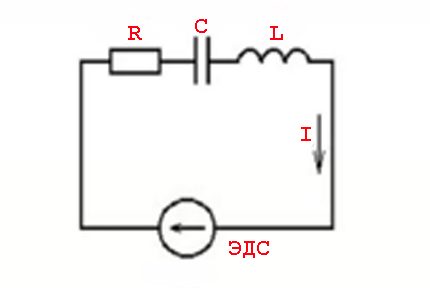
Başka bir deyişle, aktif (dirençli) ve reaktif (endüktif veya kapasitif) kapasitelerin ortaya çıkmasıyla birlikte akım değerlerinin voltaj değerlerinden ilerlemesinin (gecikmesi) bir etkisi vardır.
Bu tür fenomenlerin hesaplanması aşağıdaki formül kullanılarak gerçekleştirilir:
Z = U / I veya Z = R + J * (XL - XC)
burada: Z - empedans; R, - aktif yük; XL , XC - endüktif ve kapasitif yük; J - katsayı.
Elemanların seri ve paralel bağlantısı
Bir elektrik devresinin elemanları (devre bölümü) için, karakteristik bir moment bir seri veya paralel bağlantıdır.
Buna göre, her bir bağlantı tipine, akım akışının ve voltaj beslemesinin farklı bir yapısı eşlik eder. Bu bağlamda, Ohm yasası, unsurları dahil etme seçeneğine bağlı olarak farklı şekillerde de geçerlidir.
Direnç Devresi
Seri bağlantıya (iki bileşenli bir devrenin bir bölümü) ilişkin olarak, aşağıdaki formül kullanılır:
- I = i1 = Ben2 ;
- U = U1 + U2 ;
- R = R1 + R2
Bu formülasyon, seri olarak bağlanan direnç bileşenlerinin sayısına bakılmaksızın, devrede akan akımın değişmediğini açıkça göstermektedir.
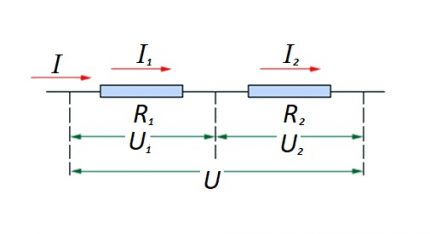
Devrenin aktif rezistif bileşenlerine uygulanan voltajın büyüklüğü, emf kaynağının toplam değerinin toplamıdır.
Her bir bileşen üzerindeki voltaj şuna eşittir: Ux = I * Rx.
Toplam direnç, devrenin tüm dirençli bileşenlerinin değerlerinin toplamı olarak düşünülmelidir.
Paralel bağlı rezistif elemanların devresi
Direnç bileşenlerinin paralel bir bağlantısının olması durumunda, aşağıdaki formül Alman fizikçi Ohm yasasına göre adil kabul edilir:
- I = i1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Paralel ve seri bağlantı kullanıldığında “karışık” tipte devre bölümlerini derleme seçenekleri göz ardı edilmez.
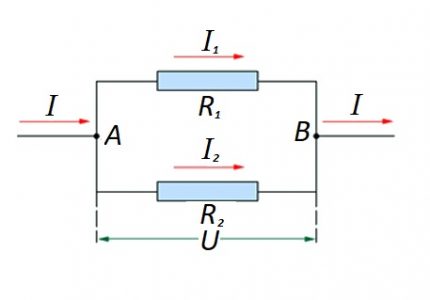
Bu seçenekler için, hesaplama genellikle paralel bağlantının direnç derecesinin ilk hesaplanmasıyla gerçekleştirilir. Ardından, seriye bağlanan direncin değeri sonuca eklenir.
İntegral ve diferansiyel hukuk biçimleri
Hesaplamalarla ilgili yukarıdaki tüm noktalar, elektrik devrelerinde "homojen" bir yapıya sahip iletkenlerin kullanıldığı koşullara uygulanabilir.
Bu arada, uygulamada, genellikle iletkenlerin yapısının farklı alanlarda değiştiği bir devrenin inşası ile uğraşmak zorundadır. Örneğin, daha büyük bir enine kesite sahip teller veya aksine, farklı malzemeler temelinde yapılan daha küçük teller kullanılır.
Bu farklılıkları açıklamak için, "Ohm'un diferansiyel-integral yasası" olarak adlandırılan bir varyasyon vardır. Sonsuz küçük bir iletken için akım yoğunluğu, mukavemet ve iletkenliğe bağlı olarak hesaplanır.
Diferansiyel hesaplama altında, formül alınır: J = ό * E
İntegral hesaplama için sırasıyla ifadeler: I * R = φ1 - φ2 + έ
Bununla birlikte, bu örnekler yüksek matematik okuluna oldukça yakındır ve gerçek uygulamada, basit bir elektrikçi aslında kullanılmamaktadır.
Konu hakkında sonuçlar ve faydalı video
Aşağıdaki videoda Ohm yasasının ayrıntılı bir analizi, nihayet bu yönde bilgiyi pekiştirmeye yardımcı olacaktır.
Tuhaf bir video dersi teorik yazılı sunumu niteliksel olarak güçlendirir:
Bir elektrikçinin çalışması veya bir elektronik mühendisinin faaliyeti, Georg Ohm yasasını yürürlükte tutmak zorunda olduğunuz anlarla ayrılmaz bir şekilde bağlantılıdır. Bunlar her profesyonelin bilmesi gereken bazı ortak gerçeklerdir.
Bu konuda kapsamlı bilgi gerekli değildir - pratikte başarılı bir şekilde uygulamak için ifadenin üç ana varyasyonunu öğrenmek yeterlidir.
Yukarıdaki materyale değerli yorumlar eklemek veya görüşünüzü belirtmek ister misiniz? Lütfen makalenin altındaki bloğa yorum yazınız. Herhangi bir sorunuz varsa, uzmanlarımıza sormaya çekinmeyin.

 Güç, akım ve gerilim nasıl hesaplanır: ev koşulları için hesaplama prensipleri ve örnekleri
Güç, akım ve gerilim nasıl hesaplanır: ev koşulları için hesaplama prensipleri ve örnekleri  Amperları Watt'a Dönüştürme: Gerilim ve akım birimlerinin dönüştürülmesine ilişkin kurallar ve pratik örnekler
Amperları Watt'a Dönüştürme: Gerilim ve akım birimlerinin dönüştürülmesine ilişkin kurallar ve pratik örnekler  Amperlerin kilowatt'a nasıl dönüştürüleceği: çeviri ilkeleri ve açıklamalarla pratik örnekler
Amperlerin kilowatt'a nasıl dönüştürüleceği: çeviri ilkeleri ve açıklamalarla pratik örnekler  Bilgisayar için kesintisiz: en iyi UPS derecesi
Bilgisayar için kesintisiz: en iyi UPS derecesi  Elektrik devrelerindeki kurallar: kod çözme grafikleri ve alfasayısal karakterler
Elektrik devrelerindeki kurallar: kod çözme grafikleri ve alfasayısal karakterler  Kilowatt'ı beygir gücüne dönüştürün: bir kW + 'da kaç ilaç ve prensipleri ve hesaplama yöntemleri
Kilowatt'ı beygir gücüne dönüştürün: bir kW + 'da kaç ilaç ve prensipleri ve hesaplama yöntemleri  Gazın özel bir eve bağlanması ne kadara mal olur: gaz arzını organize etmenin fiyatı
Gazın özel bir eve bağlanması ne kadara mal olur: gaz arzını organize etmenin fiyatı  Kurutmalı en iyi çamaşır makineleri: model derecesi ve müşteri ipuçları
Kurutmalı en iyi çamaşır makineleri: model derecesi ve müşteri ipuçları  Işığın renk sıcaklığı ve ihtiyaçlarınıza göre lambaların sıcaklığını seçme nüansları nedir
Işığın renk sıcaklığı ve ihtiyaçlarınıza göre lambaların sıcaklığını seçme nüansları nedir  Bir dairede gayzer değiştirilmesi: yedek evraklar + temel normlar ve gereksinimler
Bir dairede gayzer değiştirilmesi: yedek evraklar + temel normlar ve gereksinimler