Llei d’Ohm per a la cadena completa i per a la secció de la cadena: escriptura de fórmules, descripció i explicació
Un electricista professional, un enginyer electrònic especialista no pot desplaçar-se per la legislació d'Ohm en les seves pròpies activitats, solucionant problemes relacionats amb la configuració, la posada a punt, la reparació de circuits electrònics i elèctrics.
En realitat, tothom necessita una comprensió d’aquesta llei. Perquè tothom a la vida quotidiana ha d’afrontar l’electricitat.
I tot i que la llei del físic alemany Ohm està prevista per un curs de secundària, a la pràctica no sempre s’estudia de manera puntual. Per tant, considerarem en el nostre material un tema rellevant per a la vida i tractarem les opcions per escriure la fórmula.
El contingut de l'article:
Secció separada i circuit elèctric complet
Tenint en compte el circuit elèctric des del punt de vista d’aplicar la llei d’Ohm al circuit, cal destacar dues possibles opcions de càlcul: per a una secció única i per a un circuit de tota marxa.
Càlcul de la secció actual del circuit elèctric
La part del circuit, per regla general, es considera part del circuit, excloent la font d'EMF, com a resistència interna addicional.
Per tant, la fórmula de càlcul, en aquest cas, sembla senzilla:
I = U / R,
On, respectivament:
- Jo - força actual;
- U - tensió aplicada;
- R - resistència.
La interpretació de la fórmula és senzilla: el corrent que circula al llarg d'una determinada part del circuit és proporcional a la tensió que se li aplica i la resistència és inversament proporcional.
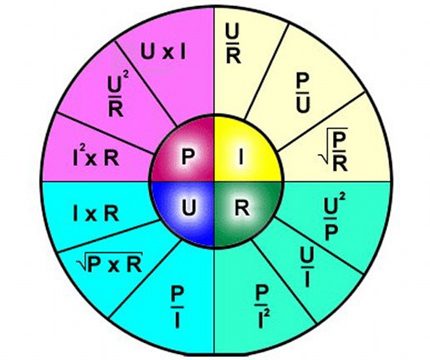
Així, la fórmula descriu clarament la dependència del corrent que circula per una secció separada del circuit elèctric respecte a certs valors de tensió i resistència.
És convenient utilitzar la fórmula, per exemple, per calcular els paràmetres de resistència, que s’han de soldar al circuit si s’especifica la tensió amb corrent.
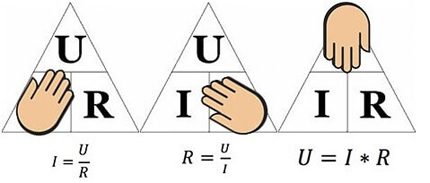
La figura anterior ajudarà a determinar, per exemple, el corrent que circula per una resistència de 10 ohms, a la qual s'aplica un voltatge de 12 volts. Substituint els valors, trobem - I = 12/10 = 1,2 amperis.
De la mateixa manera, es resolen les tasques de trobar resistència (quan es coneix corrent amb tensió) o tensió (quan es coneix tensió amb corrent).
Així, sempre és possible seleccionar la tensió de funcionament requerida, l’amperatge requerit i l’element resistent òptim.
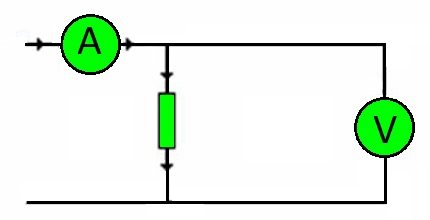
Per cert, els cables de connexió de qualsevol circuit són resistència. La magnitud de la càrrega que han de suportar està determinada per la tensió.
D’acord amb això, de nou amb la llei d’Ohm, és possible seleccionar amb precisió la secció de conductor necessària, depenent del material del nucli.
Tenim instruccions detallades al lloc web secció de cable per potència i corrent.
Opció de càlcul per a cadena completa
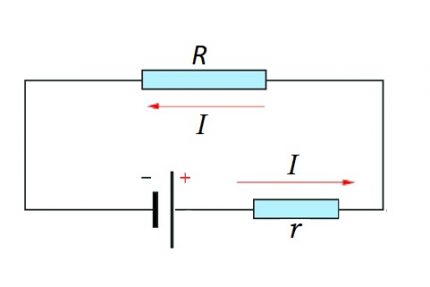
Una cadena completa ja és el lloc (s), així com la font d'EMF. És a dir, de fet, la resistència interna de la font d'EMF s'afegeix al component resistiu existent de la secció del circuit.
Per tant, és lògic que es faci un canvi a la fórmula anterior:
I = U / (R + r)
Per descomptat, el valor de la resistència interna de l’EMF en la llei d’Ohm per a un circuit elèctric complet pot ser considerat negligible, encara que en molts aspectes aquest valor de resistència depèn de l’estructura de la font d’EMF.
Tanmateix, quan es calculen circuits electrònics complexos, circuits elèctrics amb molts conductors, la presència de resistència addicional és un factor important.
Tant per a la secció del circuit com per al circuit complet, s’ha de tenir en compte el moment natural: l’ús d’una corrent constant o variable.
Si es consideraven els punts anotats anteriorment, característics de la llei d'Ohm, des del punt de vista de l'ús de corrent directe, d'acord amb el corrent altern tot sembla una mica diferent.
Consideració de la llei a una variable
El concepte de "resistència" a les condicions de pas de corrent altern hauria de considerar-se més que el concepte d '"impedància". Es tracta d’una combinació de la càrrega resistiva activa (Ra) i la càrrega formada per la resistència reactiva (Rr).
Aquests fenòmens són causats pels paràmetres dels elements inductius i les lleis de commutació segons s'apliquen a un valor de tensió variable: un valor de corrent sinusoïdal.
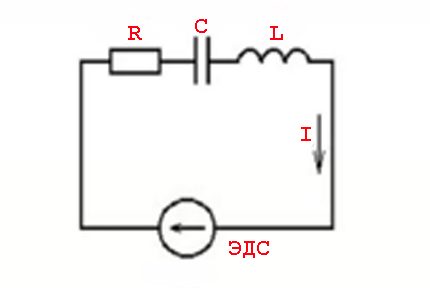
És a dir, hi ha un efecte d’avançar (retardar) els valors actuals a partir dels valors de tensió, que s’acompanya de l’aparició de capacitats actives (resistives) i reactives (inductives o capacitives).
El càlcul d'aquests fenòmens es realitza mitjançant la fórmula:
Z = U / I o Z = R + J * (XL - XC)
on: Z - impedància; R - càrrega activa; XL , XC - càrrega inductiva i capacitiva; J - coeficient.
Connexió de sèries i paral·leles d’elements
Per a elements d’un circuit elèctric (secció de circuit), un moment característic és una connexió en sèrie o paral·lela.
En conseqüència, cada tipus de connexió va acompanyada d'una naturalesa diferent del subministrament de corrent i tensió. En aquest sentit, la llei d'Ohm també s'aplica de maneres diferents, depenent de l'opció d'incloure elements.
Circuit de resistència
En relació amb una connexió en sèrie (una secció d'un circuit amb dos components), s'utilitza la fórmula següent:
- I = i1 = Jo2 ;
- U = U1 + U2 ;
- R = R1 + R2
Aquesta formula demostra clarament que, independentment del nombre de components resistents connectats en sèrie, el corrent que circula al circuit no canvia.
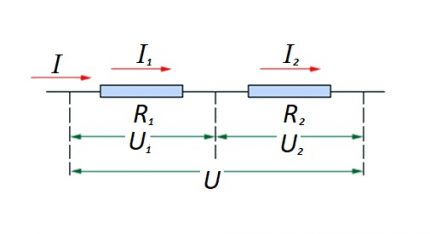
La magnitud del voltatge aplicat als components resistents actius del circuit és la suma del valor total de la font emf.
La tensió de cada component individual és igual a: Ux = I * Rx.
Cal considerar la resistència total com la suma de les qualificacions de tots els components resistents del circuit.
Circuit d’elements resistents connectats en paral·lel
En el cas que hi hagi una connexió paral·lela de components resistents, la fórmula següent es considera justa respecte a la llei del físic alemany Ohm:
- I = i1 + Jo2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
No es descarta les opcions per a la compilació de seccions de circuit de tipus “mixt” quan s’utilitzen connexions paral·leles i en sèrie.
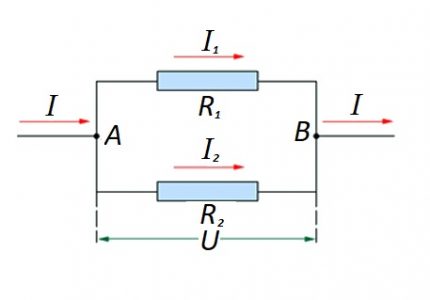
Per a aquestes opcions, el càlcul es realitza generalment mitjançant el càlcul inicial de la qualificació resistiva de la connexió paral·lela. Aleshores, s’afegeix al resultat el valor de la resistència connectada en sèrie.
Formes de dret integrals i diferencials
Tots els punts anteriors amb els càlculs són aplicables a condicions quan s'utilitzen conductors d'una estructura "homogènia" als circuits elèctrics.
Mentrestant, a la pràctica, sovint s’ha d’afrontar la construcció d’un circuit on l’estructura dels conductors canviï en diferents àrees. Per exemple, s’utilitzen cables d’una secció més gran o, per contra, d’altres més petits, realitzats a partir de diferents materials.
Per tenir en compte aquestes diferències, hi ha una variació de l'anomenada "llei diferencial-integral d'Ohm". Per a un conductor infinitament petit, el nivell de densitat actual es calcula segons la força i la conductivitat.
En el càlcul diferencial, es pren la fórmula: J = ό * E
Per al càlcul integral, respectivament, la redacció: I * R = φ1 - φ2 + έ
Tanmateix, aquests exemples estan més a prop de l'escola de matemàtiques superiors i, en la pràctica real, no es fa servir un electricista simple.
Conclusions i vídeo útil sobre el tema
Una anàlisi detallada de la llei d'Ohm al vídeo següent ajudarà a consolidar finalment el coneixement en aquesta direcció.
Una peculiar lliçó de vídeo reforça qualitativament la presentació escrita teòrica:
La feina d’un electricista o l’activitat d’un enginyer electrònic està vinculada indestriablement a moments en què realment heu d’observar la llei de Georg Ohm en acció. Aquestes són algunes veritats comunes que tot professional hauria de conèixer.
No es requereix un coneixement àmplia sobre aquesta qüestió: n’hi ha prou per aprendre les tres principals variacions de la redacció per aplicar-les amb èxit a la pràctica.
Voleu complementar el material anterior amb comentaris valuosos o expressar la vostra opinió? Si us plau, escriu comentaris al bloc de l'article. Si teniu cap pregunta, no dubteu en preguntar als nostres experts.

 Com calcular potència, corrent i tensió: principis i exemples de càlcul per a condicions domèstiques
Com calcular potència, corrent i tensió: principis i exemples de càlcul per a condicions domèstiques  Conversió d'amperis a Watts: regles i exemples pràctics de la conversió de les unitats de corrent i tensió
Conversió d'amperis a Watts: regles i exemples pràctics de la conversió de les unitats de corrent i tensió  Com convertir els amperis a quilowatts: principis de traducció i exemples pràctics amb explicacions
Com convertir els amperis a quilowatts: principis de traducció i exemples pràctics amb explicacions  Ininterrompuda per a l’ordinador: qualificació dels millors SAI
Ininterrompuda per a l’ordinador: qualificació dels millors SAI  Convencions en circuits elèctrics: gràfics de descodificació i caràcters alfanumèrics
Convencions en circuits elèctrics: gràfics de descodificació i caràcters alfanumèrics  Convertiu quilowatts en cavalls de potència: quants medicaments en un kW + principis i mètodes de càlcul
Convertiu quilowatts en cavalls de potència: quants medicaments en un kW + principis i mètodes de càlcul  Quant costa connectar el gas a una casa privada: el preu de l’organització del subministrament de gas
Quant costa connectar el gas a una casa privada: el preu de l’organització del subministrament de gas  Les millors rentadores amb assecador: valoració del model i consells per al client
Les millors rentadores amb assecador: valoració del model i consells per al client  Quina és la temperatura del color de la llum i els matisos de l’elecció de la temperatura de les làmpades en funció de les vostres necessitats
Quina és la temperatura del color de la llum i els matisos de l’elecció de la temperatura de les làmpades en funció de les vostres necessitats  Substitució d’un guèiser en un apartament: documentació de substitució + normes bàsiques i requisits
Substitució d’un guèiser en un apartament: documentació de substitució + normes bàsiques i requisits