Ohmos dėsnis visai grandinei ir grandinės daliai: formulių rašymas, aprašymas ir paaiškinimas

Profesionalus elektrikas, specialistas elektronikos inžinierius negali apeiti Ohmo įstatymų vykdydamas savo veiklą, spręsdamas bet kokias problemas, susijusias su elektroninių ir elektros grandinių nustatymu, derinimu, taisymu.

Tiesą sakant, visiems reikia šio įstatymo supratimo. Nes kiekvienas kasdieniame gyvenime turi susidurti su elektra.

Ir nors vokiečių fiziko Ohmo įstatymą numato vidurinės mokyklos kursai, praktikoje jis ne visada mokomasi laiku. Todėl savo medžiagoje mes apsvarstysime tokią temą, kuri yra aktuali gyvenimui, ir nagrinėsime formulės rašymo variantus.

Atskiras skyrius ir visa elektros grandinė

Atsižvelgiant į elektrinę grandinę Ohmo dėsnio taikymo grandinei požiūriu, reikia atkreipti dėmesį į du galimus skaičiavimo variantus: vienai sekcijai ir visavertei grandinei.

Elektros grandinės srovės ruožo apskaičiavimas

Grandinės dalis, kaip taisyklė, yra laikoma grandinės dalimi, išskyrus EMF šaltinį, turinčią papildomą vidinį pasipriešinimą.

Todėl skaičiavimo formulė šiuo atveju atrodo paprasta:

I = U / R,

Kur atitinkamai:

• Aš - srovės stipris;
• U - taikoma įtampa;
• R - pasipriešinimas.

Formulės aiškinimas yra paprastas - srovė, tekanti išilgai tam tikros grandinės dalies, yra proporcinga jai taikoma įtampa, o varža yra atvirkščiai proporcinga.

Vadinamasis grafinis „ramunė“, per kurį pateikiamas visas formuluotės variantų rinkinys, pagrįstas Ohmo įstatymais. Patogus įrankis kišenėms laikyti: „P“ sektorius - galios formulės; sektorius „U“ - įtampos formulės; sektorius „I“ - dabartinės formulės; sektorius „R“ - pasipriešinimo formulės

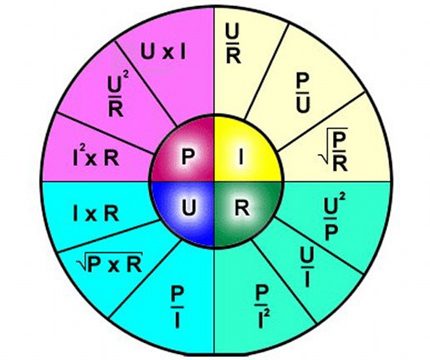
Taigi formulė aiškiai apibūdina srovės, tekančios per atskirą elektros grandinės skyrių, priklausomybę nuo tam tikrų įtampos ir varžos verčių.

Patogu naudoti formulę, pavyzdžiui, apskaičiuojant pasipriešinimo parametrus, kurie turi būti išlydomi į grandinę, jei nurodyta įtampa su srove.

Ohmo dėsnis ir dvi pasekmės, kurias privalo turėti kiekvienas profesionalus elektrikas, elektros inžinierius, elektronikos inžinierius ir kiekvienas, susijęs su elektros grandinių darbu. Iš kairės į dešinę: 1 - srovės aptikimas; 2 - atsparumo nustatymas; 3 - įtampos nustatymas, kur I - srovės stipris, U - įtampa, R - varža

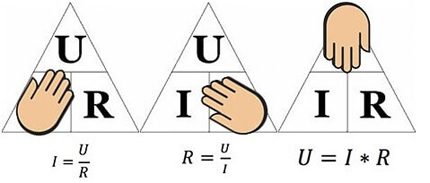
Aukščiau pateiktas paveikslėlis padės nustatyti, pavyzdžiui, srovę, tekančią per 10 omų varžą, kuriai taikoma 12 voltų įtampa. Pakeitę reikšmes randame - I = 12/10 = 1,2 amperų.

Panašiai sprendžiamos varžos (kai žinoma srovė su įtampa) arba įtampos (kai įtampa su srove žinomos) užduotys.

Taigi visada galima pasirinkti reikiamą darbinę įtampą, reikiamą srovės stiprį ir optimalų varžinį elementą.

Siūloma naudoti formulė nereikalauja atsižvelgti į įtampos šaltinio parametrus. Tačiau grandinė, kurioje yra, pavyzdžiui, akumuliatorius, bus apskaičiuojama pagal kitą formulę. Diagramoje: A - ampermetro įtraukimas; V - voltmetro įtraukimas.

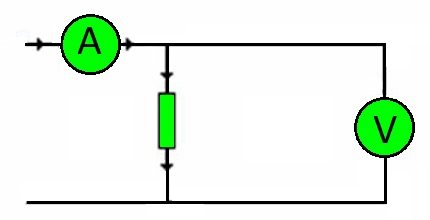
Beje, bet kurios grandinės jungiamieji laidai yra atsparūs. Apkrovos, kurią jie turi patirti, dydį lemia įtampa.

Atitinkamai, vėlgi naudojant Ohmo dėsnį, tampa įmanoma tiksliai parinkti reikiamą laidininko skerspjūvį, atsižvelgiant į šerdies medžiagą.

Mes turime išsamias instrukcijas svetainėje kabelio skerspjūvis pagal galią ir srovę.

Skaičiavimo parinktis visai grandinei

Visa grandinė jau yra svetainė (-ės), taip pat EML šaltinis. Tai yra, iš tikrųjų EML šaltinio vidinė varža pridedama prie esamo grandinės sekcijos varžinio komponento.

Todėl kai kurie minėtos formulės pakeitimai yra logiški:

I = U / (R + r)

Žinoma, EML vidinės EML vidinės varžos vertė, atsižvelgiant į visą elektros grandinę, gali būti laikoma nereikšminga, nors daugeliu atžvilgių ši varžos vertė priklauso nuo EML šaltinio struktūros.

Tačiau, skaičiuojant sudėtingas elektronines grandines, elektros grandines su daugybe laidininkų, svarbus veiksnys yra papildomos varžos buvimas.

Atliekant skaičiavimus visavertėje elektros grandinėje, visada atsižvelgiama į EML šaltinio varžinę vertę. Ši vertė pridedama prie pačios elektros grandinės varžos. Diagramoje: I - srovės srautas; R yra varžinisis elementas išorinis; r yra EML (energijos šaltinio) varžinis faktorius

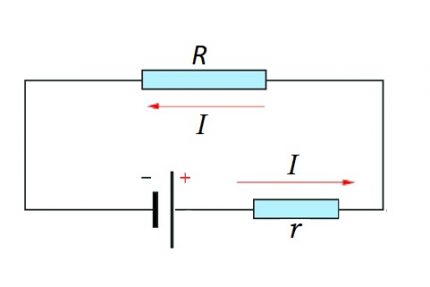
Tiek grandinės sekcijai, tiek visai grandinei reikia atsižvelgti į natūralų momentą - nuolatinės arba kintamos srovės naudojimą.

Jei aukščiau paminėti taškai, būdingi Ohmo dėsniui, buvo nagrinėjami nuolatinės srovės naudojimo požiūriu, atitinkamai su kintama srove viskas atrodo šiek tiek kitaip.

Įstatymo laikymasis kintamajam

„Atsparumo“ kintamosios srovės praleidimo sąlygoms sąvoka turėtų būti laikoma labiau kaip „varžos“ sąvoka. Tai yra aktyviosios varžinės apkrovos (Ra) ir reaktyviojo varžos (Rr) sukeltos apkrovos derinys.

Tokius reiškinius sukelia indukcinių elementų parametrai ir perjungimo dėsniai, taikomi kintamai įtampos vertei - sinusoidinei srovės vertei.

Panašu, kad tai ekvivalentinė kintamos srovės elektros grandinė, naudojama skaičiavimams, pagrįstiems Ohmo dėsnio principais: R - varžinis komponentas; C yra talpinis komponentas; L yra indukcinis komponentas; EML yra energijos šaltinis; I srovės srautas

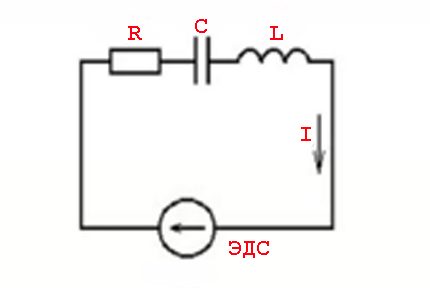
Kitaip tariant, atsiranda įtampos verčių padidėjimas (atsilikimas), o tai reiškia, kad atsiranda aktyviosios (varžinės) ir reaktyviosios (induktyvinės ar talpinės) talpos.

Tokie reiškiniai apskaičiuojami pagal formulę:

Z = U / I arba Z = R + J * (X_L - X_C)

kur: Z - varža; R - aktyvus krūvis; X_L , X_C - indukcinė ir talpinė apkrova; J - koeficientas.

Elementų serijos ir lygiagrečios jungtys

Elektros grandinės elementams (grandinės sekcijai) būdingas momentas yra nuoseklioji arba lygiagreti jungtis.

Atitinkamai, kiekvieną jungties tipą lydi skirtingas srovės srautas ir įtampos tiekimas. Šiuo atžvilgiu Ohmo įstatymai taip pat taikomi skirtingais būdais, atsižvelgiant į galimybę įtraukti elementus.

Rezistoriaus grandinė

Atliekant nuoseklųjį jungimą (grandinės dalį su dviem komponentais) naudojama ši formulė:

• I = i₁ = Aš₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Ši formuluotė aiškiai parodo, kad, nepaisant nuosekliai sujungtų varžinių komponentų skaičiaus, grandinėje tekanti srovė nesikeičia.

Varžtinių elementų sujungimas grandinės sekcijoje nuosekliai. Šiai galimybei taikomas jos apskaičiavimo įstatymas. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U, U1, U2 - taikoma įtampa

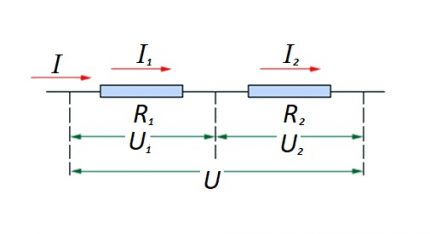
Įtampos dydis, taikomas aktyviosioms varžinėms grandinės dalims, yra visos EMF šaltinio vertės suma.

Kiekvieno atskiro komponento įtampa lygi: Ux = I * Rx.

Bendras atsparumas turėtų būti laikomas visų grandinės varžinių komponentų vardinių verčių suma.

Lygiagrečiai sujungtų varžinių elementų grandinė

Tuo atveju, kai yra lygiagretus varžos komponentų sujungimas, ši formulė laikoma teisinga vokiečių fiziko Ohmo įstatymų atžvilgiu:

• I = i₁ + Aš₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Neatmetamos „mišraus“ tipo grandinių sekcijų sudarymo galimybės, kai naudojamas lygiagretus ir nuoseklus ryšys.

Atspariųjų elementų sujungimas grandinėje lygiagrečiai vienas su kitu. Šiai galimybei taikomas jos apskaičiavimo įstatymas. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U yra suminė įtampa; A, B - įėjimo / išėjimo taškai

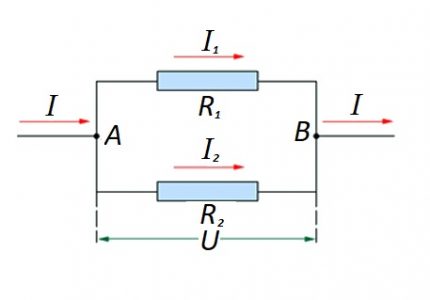
Tokioms parinktims skaičiavimas paprastai atliekamas iš pradžių apskaičiuojant lygiagrečiojo jungimo varžą. Tada prie rezultato pridedama nuosekliai sujungto rezistoriaus vertė.

Integrali ir diferencinė teisės formos

Visi aukščiau išvardinti skaičiavimų punktai yra taikomi esant sąlygoms, kai elektros grandinėse naudojami „vienalytės“ struktūros laidininkai.

Tuo tarpu praktikoje dažnai tenka susidurti su grandinės statyba, kai laidininkų struktūra keičiasi skirtingose ​​vietose. Pavyzdžiui, naudojami didesnio skerspjūvio laidai arba, priešingai, mažesni, pagaminti iš skirtingų medžiagų.

Norint atsižvelgti į tokius skirtumus, egzistuoja vadinamojo Ohmo diferencinio integralo dėsnio variantas. Be galo mažam laidininkui srovės tankis apskaičiuojamas priklausomai nuo stiprio ir laidumo.

Atliekant diferencinį skaičiavimą, naudojama formulė: J = ό * E

Atliekant vientisą skaičiavimą, formuluotė: I * R = φ1 - φ2 + έ

Tačiau šie pavyzdžiai yra gana artimi aukštosios matematikos mokyklai ir realioje praktikoje paprastas elektrikas faktiškai nenaudojamas.

Išvados ir naudingas vaizdo įrašas šia tema

Žemiau esančiame vaizdo įraše pateikta išsami Ohmo įstatymo analizė padės galutinai įtvirtinti žinias šia linkme.

Savotiška vaizdo pamoka kokybiškai sustiprina teorinį pristatymą raštu:

Elektriko darbas ar elektronikos inžinieriaus veikla yra neatsiejamai susiję su akimirkomis, kai iš tikrųjų reikia laikytis Georgo Ohmo įstatymo. Tai yra kelios bendrosios tiesos, kurias turėtų žinoti kiekvienas profesionalas.

Plačių žinių šiuo klausimu nereikia - norint sėkmingai pritaikyti praktikoje, pakanka išmokti tris pagrindinius formuluotės variantus.

Ar norite papildyti aukščiau pateiktą medžiagą vertingais komentarais ar pareikšti savo nuomonę? Prašau parašyti komentarus bloke po straipsniu. Jei turite klausimų, nedvejodami kreipkitės į mūsų ekspertus.